How do you find the roots for #f(x) = 6x^4 – 2x – 15# using the fundamental theorem of algebra?
2 Answers
The FTOA only tells us that
Using Descartes' Rule of Signs we can determine that it has two real zeros and a pair of complex zeros.
Explanation:
The Fundamental Theorem of Algebra (FTOA) only tells you how many roots a polynomial has - not how to find them.
Specifically the FTOA tells us that any non-constant polynomial in a single variable with Complex (possibly Real) coefficients has a Complex (possibly Real) zero.
A straightforward corollary of that, often stated as part of the FTOA is that a single variable polynomial of degree
In our example:
#f(x) = 6x^4-2x-15#
is a quartic polynomial - i.e. is of degree
So the FTOA tells us that it has exactly
We can use Descartes' Rule of Signs to find that
All of these zeros are irrational and have a quite messy radical form.
Durand-Kerner
We can find numerical approximations for the roots using a numerical method such as the Durand-Kerner method.
In the given example, we can use a program such as this one (written in C++):

and hence find approximate zeros:
#x_1 ~~ 1.30904#
#x_2 ~~ -1.20363#
#x_(3,4) ~~ -0.0527043+-1.25854i#
See https://socratic.org/s/aEgiJEsx for more information.
Algebraic method
Since the given quartic has no term in
#6x^4-2x-15 = 6(x^2-ax+b)(x^2+ax+c)#
#color(white)(6x^4-2x-15) = 6x^4+6(b+c-a^2)x^2+6a(b-c)x+6bc#
Hence, equating the coefficients of
#{ (b+c = a^2), (b-c = -1/(3a)), (bc = -5/2) :}#
Then:
#(a^2)^2 = (b+c)^2 = (b-c)^2+4bc = 1/(9(a^2))-10#
Hence we get a cubic in
From the resulting values for
Messy, but works.
See below.
Explanation:
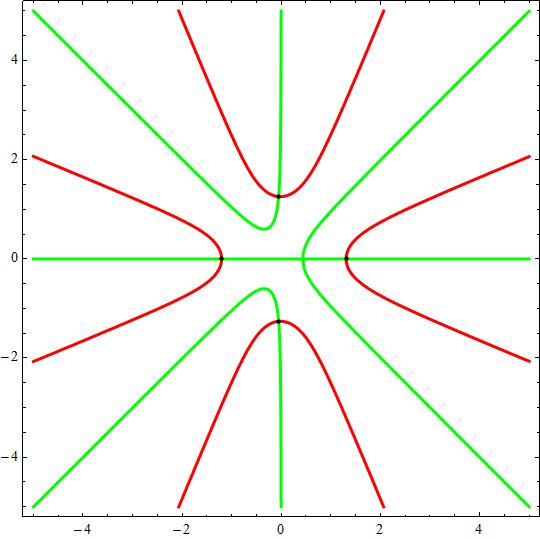
As Gauss did at his time, taking
and making
and representing the curves
the roots can be observed at the intersection points for red's and green's