What is the value of x?
A. 6
B. 6√2
C. 12
D. 12√2
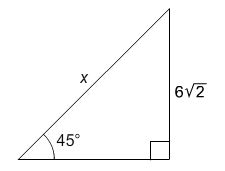 .
.
A. 6
B. 6√2
C. 12
D. 12√2
.
2 Answers
Explanation:
We know an angle in the triangle and we know the opposite side. What we want to know is the hypotenuse length. There are two ways to do this, the first one is used for any problem like this, but the second simply comes about since we are dealing with a 45 degree angle.
The first technique uses
Your answer is C. But let's explore the second method.
45/45/90 right triangles have a special interaction where both side legs (those not the hypotenuse) are identical. This is proven with interactions with
Explanation:
In a triangle with angles
The image shows us that the shorter sides have length


