How to you find the derivative of a sine function and a cosine function?
2 Answers
I used a slightly different approach....
Explanation:
There is a "right" mathematically correct method to evaluate the derivatives of these two functions...but....it is a bit complicated and everybody normally forget it immediately...!
Here as a challenge I want to show you a "visual" method that I always found really interesting and easy to remember.
The derivative of your function represents the "inclination" of your function at each point. Basically you can imagine that at every point of your function you can put a tangent line whose slope will be the derivative!
Now let us see our two functions and their inclinations:
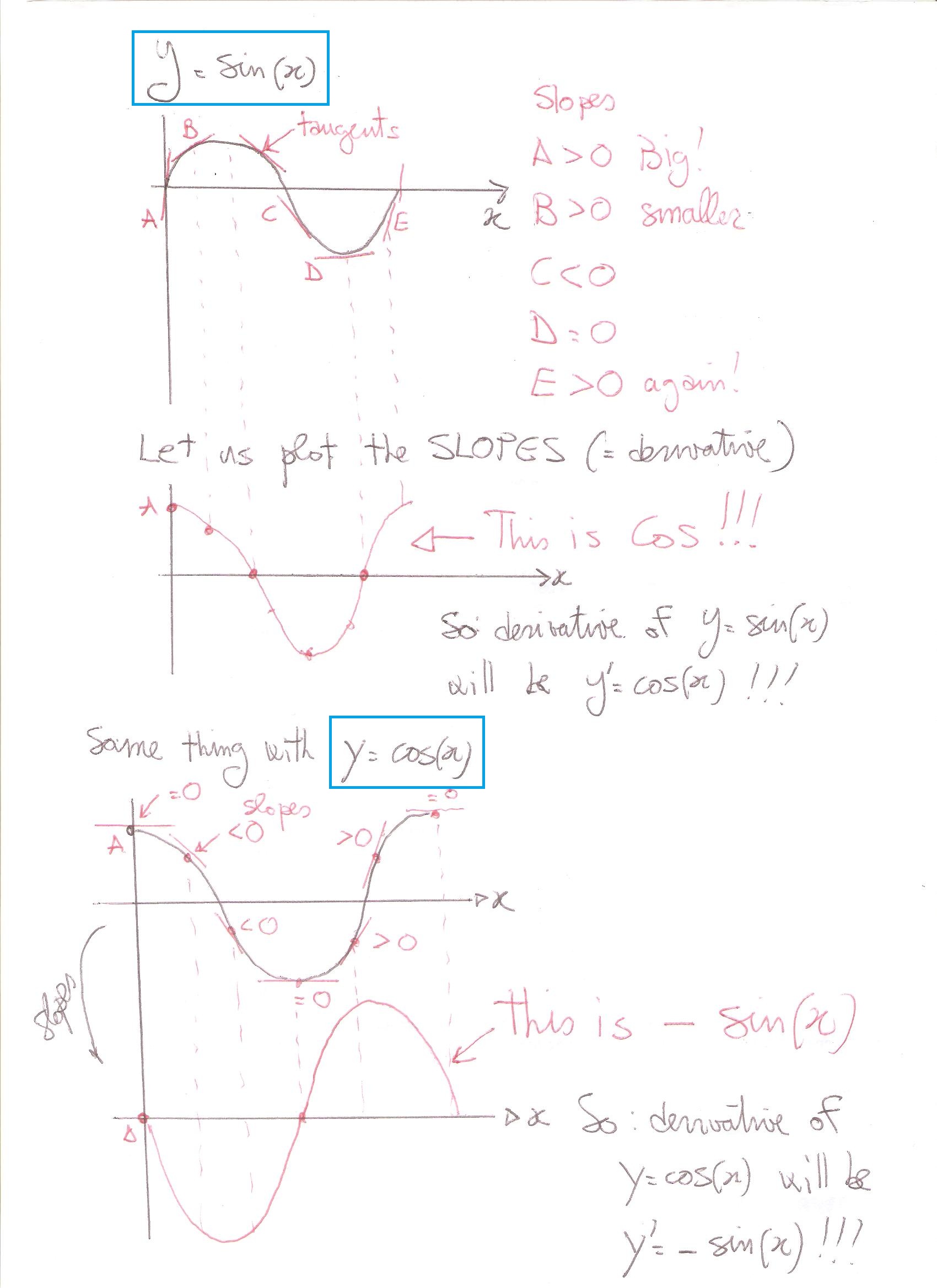
Anyway, you can find the rigorous proof at:
By definition the derivative of a function
Consider
Use now the trigonometric formula for the sine of the sum of two angles:
and we have:
simplify and regroup:
We know that:
So:
Consider now
and use the trigonometric formula for the cosine of the sum of two angles:
and we have:
simplify and regroup:
We know that:
So:


