What is the formula for determine heating produce by a lens?
1 Answer
Let
#r# be radius of the lens. As such its area is#=pir^2# #W# be average intensity of solar radiation reaching earth's surface#P_(IR)# be percent composition of Infrared energy (component responsible for generating heat) of#W# #T# be transmission coefficient or transmittance of lens material.#A# be absorption coefficient of the lens material.
Assuming perpendicular incidence angle of light on the lens surface and ignoring scattering.
Amount of heat arriving at the focus of lens is
.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-
Value of
Sunlight reaching at Earth's surface is around
When light strikes a glass surface, some of the incident light is reflected. The amount of reflected light depends on the angle of incidence and on the refractive indices of the glass and the medium in which glass is located (e.g., air). The fraction of the reflected and transmitted light can be determined using the Fresnel equations. For a angle of incidence being perpendicular to the glass surface, the fraction of reflected light is given by the reflection coefficient or reflectance
If
Reflection Coefficient or Reflectance
As the light passes through glass (lens here) it is not only reflected at the front surface, but also from the rear surface. In real life, light could be reflected back and forth several times.
Therefore, the total reflectance through a glass can be written as
# (2R) / (1+R)#
If absorption and scattering are neglected, then the transmission coefficient or transmittance
#T=1-R#
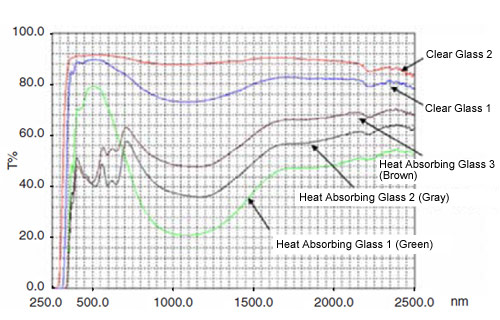
From representative transmittance graph above a value of
The absorbance for a specific glass is shown in figure below. Absorbance is used to describe the decrease in intensity of light as it travels through the glass. It is defined as
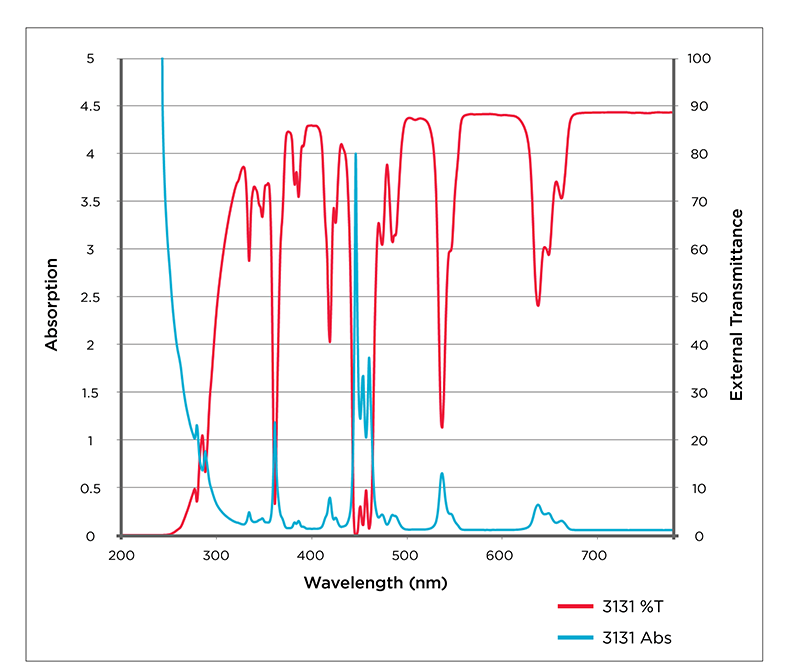
As light travels through glass, the intensity of the light is typically reduced. When energy of a photon of light equals the excitation energy of an electron within the glass to its higher energy state the photon is absorbed by the glass.
It depends on the composition and thickness of the glass as well as the wavelength of incident light.
For our lens a value of
