#A# is a set containing certain elements. How do we define #A'#?
Let us consider a universal set #U#, which is set of all the possible elements. Now as #A# contains some elements, #A'# is its complementary set which contains all the elements, other than those contained in #A#.
In other words #A subU#, #A'subU#, but #AuuA'=U# and #AnnA'=phi#. In other words #A# and #A'# together contain all the elements in the universal set #U#, but there is no element common between #A# and #A'#. In venn diagram we describe it as under:
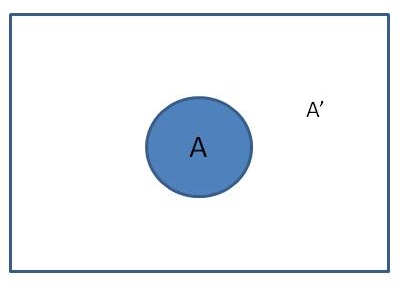
Now as #AsubB#, let #B# and #B'# be as shown below.
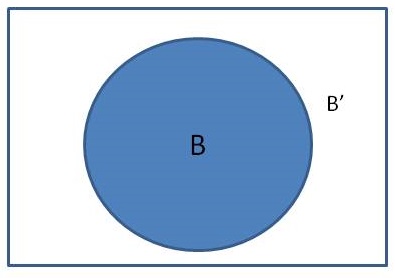
Further as #AsubB#, we have #AnnB=A#
Comparing #A'# and #B'#, it is apparent that #A'# contains all the elements #B'# and additionally those as well which are contained in #B# but not #A#.
Hence #B'subA'#


