First, graph #r=2cos(3theta)# to get an idea of what the petals look like. It can be really helpful to draw concentric circles and radial angle lines on graph paper, so that you have a polar graph, like this:
Next, using either a graphing utility or this graph paper, plot the graph using convenient points.
#{:(theta,r),(--,--),(0,2),(+-pi/12,+-sqrt(2)~~+-1.41),(+-pi/8,+-sqrt(2-sqrt(2))~~+-0.77),(+-pi/6,0):}#
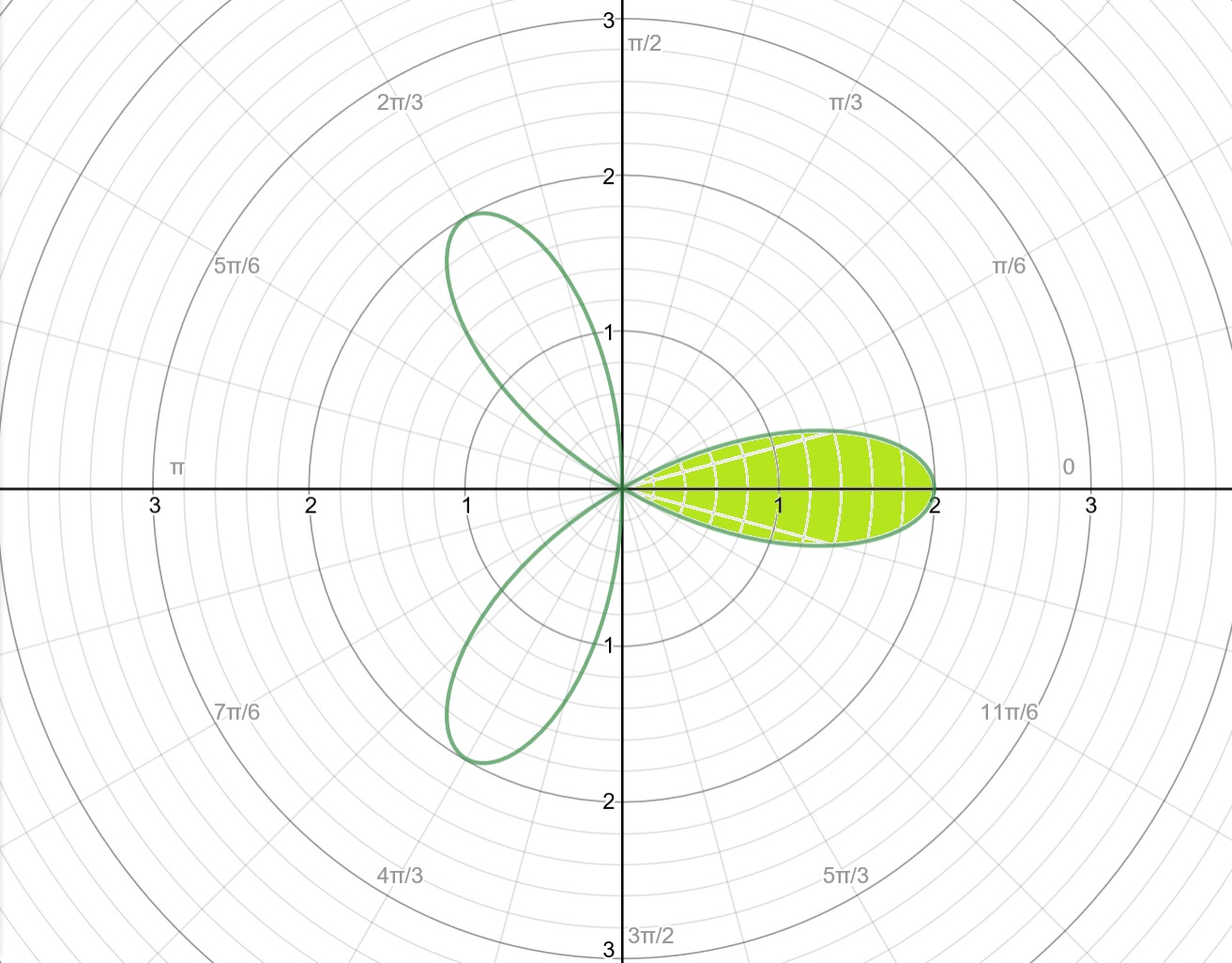
The area of a petal can be determined by an integral of the form
#A=1/2int_alpha^betar(theta)^2 d theta#
Notice the petal in Quadrant I and IV does not extend past #+-pi/6# and that it is perfectly split between the two quadrants. That implies that if we can find the are of just half a petal, then we can multiply the result by two and get the area of the entire petal.
Letting the interval of integration go from #theta=0# to #theta=pi/6# and doubling the entire integration gives
#A=2xx1/2int_0^(pi/6)4cos^2(3theta)d theta#
#A=4int_0^(pi/6)cos^2(3theta)d theta#
The half-angle identity for cosine says
#cos^2(u)=(1+cos(2u))/2#, so
#cos^2(3theta)=(1+cos(6theta))/2#.
This changes our integral to
#A=4int_0^(pi/6)(1+cos(6theta))/2d theta#
#A=2int_0^(pi/6)(1+cos(6theta))d theta#
#A=2int_0^(pi/6)d theta+2int_0^(pi/6)cos(6theta)d theta#
Using #u#-substitution, you can determine the integral of the cosine function.
#A=2[theta]_0^(pi/6)+2[1/6sin(6theta)]_0^(pi/6)#
#A=pi/3#


