Question

How do you find the gradient of the curve `y=(3x-9)/(2x^2)` at the point where the curve crosses the `x`-axis?

Answer 1

When the curve crosses the x-axis, the gradient of the curve is `1/6`.

Explanation:

Given-

`y=(3x-9)/(2x^2)`

The curve crosses the x-axis at `y=0`

Then -

`(3x-9)/(2x^2)=y`
`(3x-9)/(2x^2)=0`
`(3x-9)=0 xx 2x^2`
`3x-9=0`
`3x=9`
`x=9/3=3`

At `x=3` the curve crosses the x-axis.

The first derivative of the given function gives the gradient of the curve at any point.

`dy/dx=[[(2x^2)(3)]-[(3x-9)(4x)]]/(2x^2)^2`

`dy/dx=[[6x^2]-[12x^2-36x]]/(4x^4)`

`dy/dx=(6x^2-12x^2+36x)/(4x^4)`

`dy/dx=(-6x^2+36x)/(4x^4)`

When the curve crosses the x-axis, the y- coordinate is 0.

At `x=3: dy/dx=(-6(3^2)+36(3))/(4(3^4))=(-54+108)/324=54/324=1/6`

When the curve crosses the x-axis, the gradient of the curve is`1/6`.

Answer 2

The gradient is `1/6`

Explanation:

The curve will cross the x-axis as an x-intercept, aka `y = 0`.

`0 = (3x - 9)/(2x^2)`

`3x - 9 = 0`

`x = 3`

We now find the derivative.

`y = (3x - 9)/(2x^2)`

`y = 3/(2x) - 9/(2x^2)`

`y = 3/2x^-1 - 9/2x^-2`

`y' = -3/2x^(-2) - 9/2(-2)x^(-3)`

`y'= 9/x^3 - 3/(2x^2)`

The slope of the tangent at that point is

`y'(3) = 9/3^3 - 3/(2(3)^2)`

`y'(3) = 1/3 - 3/(18)`

`y'(3) = 1/3 - 1/6`

`y'(3) = 1/6`

Here is the graph of the function with the tangent at `x = 3`.

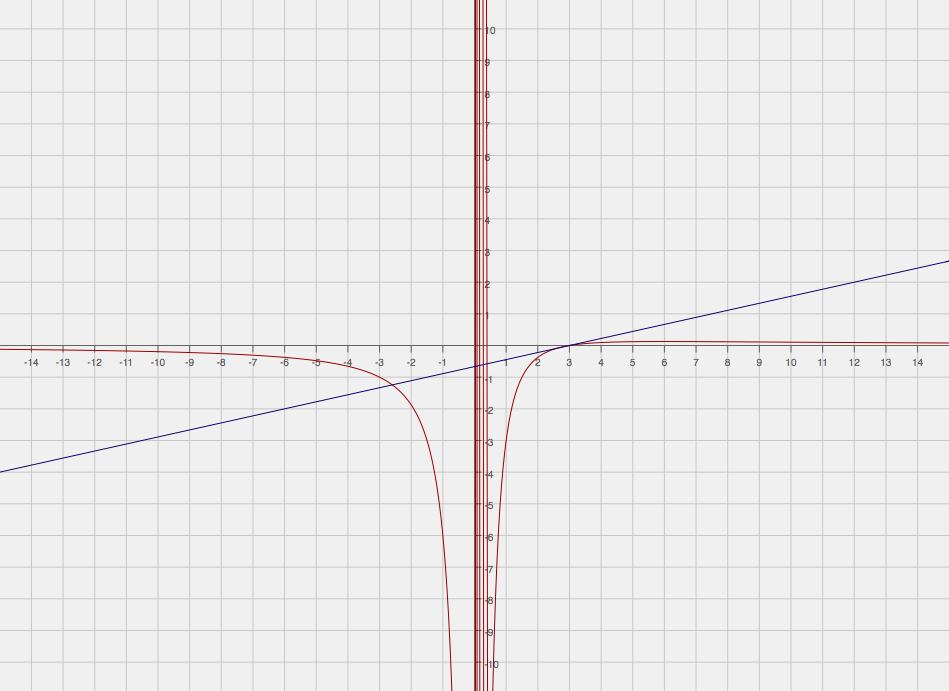
Hopefully this helps!