How do you ise interval notation indicate where f(x) is concave up and concave down for #f(x)=x^(4)-6x^(3)#?
1 Answer
Explanation:
What you want to do is find the second derivative using the power rule:
The first derivative is:
The second derivative is:
What you want to do now is factor it and set it equal to zero:
Now you make a test interval from:
You test values from the left and right into the second derivative but not the exact values of
If you get a negative number then it means that at that interval the function is concave down and if it's positive its concave up.
If done so correctly you should get that:
You should also note that the points
Attached below is a picture that may help you:
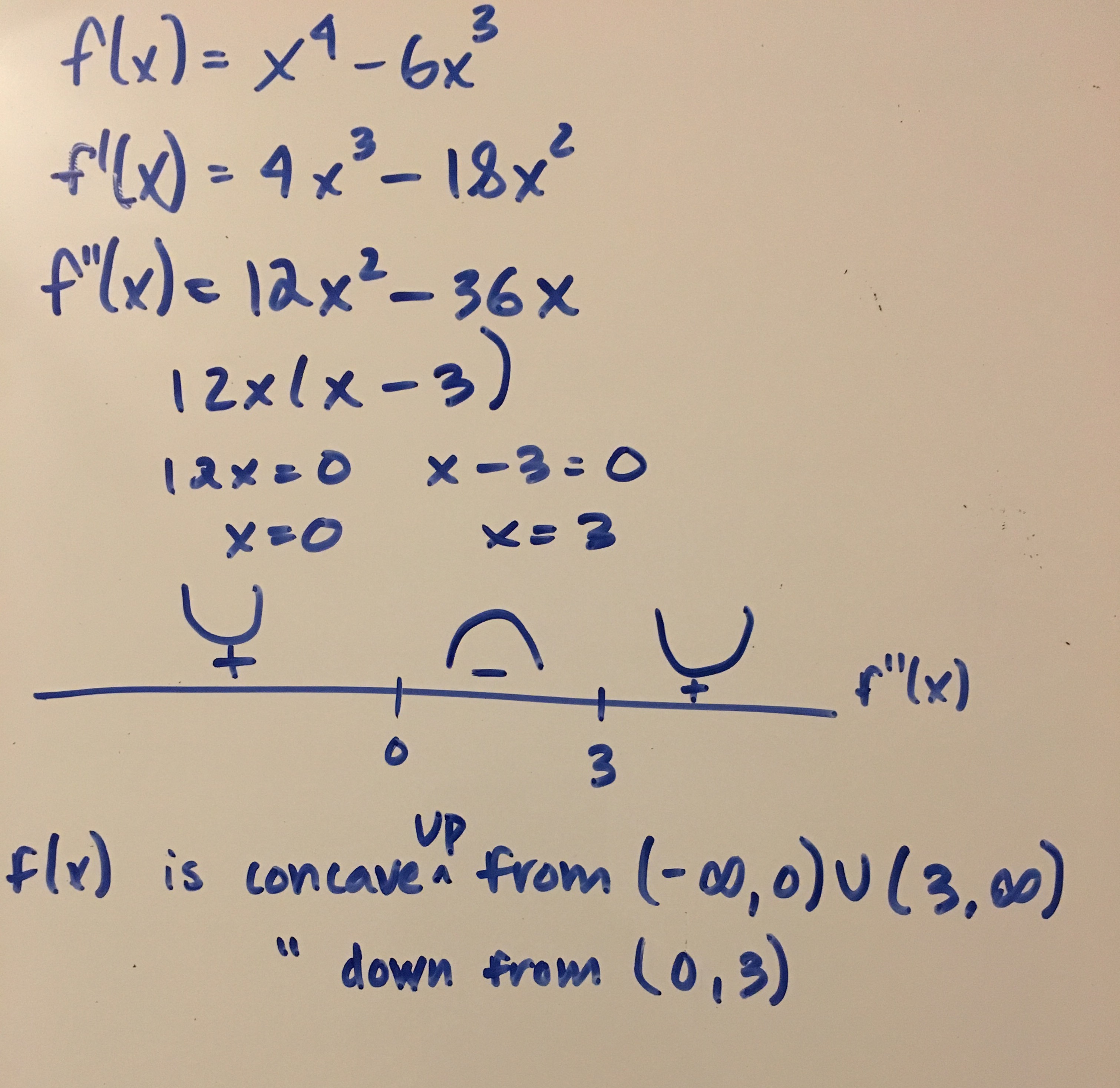
The graph may also help you:
graph{x^4-6x^3 [-147.3, 145, -125.6, 20.5]}

