Which of the following is NOT a valid quantum number set for an orbital?
Is #A# wrong?
#A)# #(n,l,m_l) = (3,-3, 2)#
#B)# #(n,l,m_l) = (4, 3, 0)#
#C)# #(n,l,m_l) = (2, 1, 1)#
#D)# #(n,l,m_l) = (3, 2, 0)#
Is
1 Answer
Jun 19, 2017
Recall the following relevant rules:
- The value of the angular momentum quantum number
#l# can at most be#n - 1# , one less than the principal quantum number#n# . Also,#l = 0, 1, 2, . . . # , so#l >= 0# . #m_l# can only be in the set#{-l, -l+1, . . . , 0, . . . , l-1, l}# . That is, the magnitude of any given#m_l# can at most be#l# .
In fact, you are correct that it is
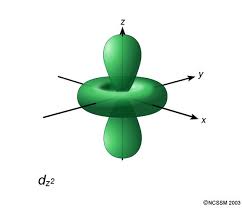
#B# specifies a#4f# orbital of#m_l = 0# , namely the#4f_(z^3)# .
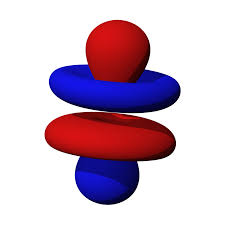
#C# specifies a#2p# orbital of#m_l = +1# , such as the#2p_x# .
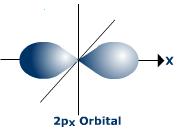
#D# specifies a#3d# orbital of#m_l = 0# , namely the#3d_(z^2)# .