In the function #f(x) = 1/(sqrt(2x))#, what is the equation of the tangent line to the graph of #f# at the point where #x=1/2#?

Question

776 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-19T22:52:09

The equation is #y = 3/2 - x#.

The y-coordinate at the point of tangency is given by

#f(1/2) = 1/sqrt(2(1/2))#

#f(1/2) = 1/sqrt(1)#

#f(1/2) = 1#

Now we find the derivative.

#f(x) = 1/(2x)^(1/2)#

#f(x) = (2x)^(-1/2)#

Using the chain and power rules:

#f'(x) = 2 *-1/2(2x)^(-3/2)#

#f'(x) = -1/(2x)^(3/2)#

Now the derivative at #x = a# will be the slope of the tangent line.

#f'(1/2) = -1/(2(1/2))^(3/2)#

#f'(1/2) = -1/1#

#f'(1/2) = -1#

We can next find the equation of the tangent line.

#y - y_1 = m(x -x_1)#

#y - 1 = -1(x - 1/2)#

#y - 1 = -x + 1/2#

#y = -x + 3/2#

Here is a graphical representation of the tangent line to the graph at #x =1/2#.

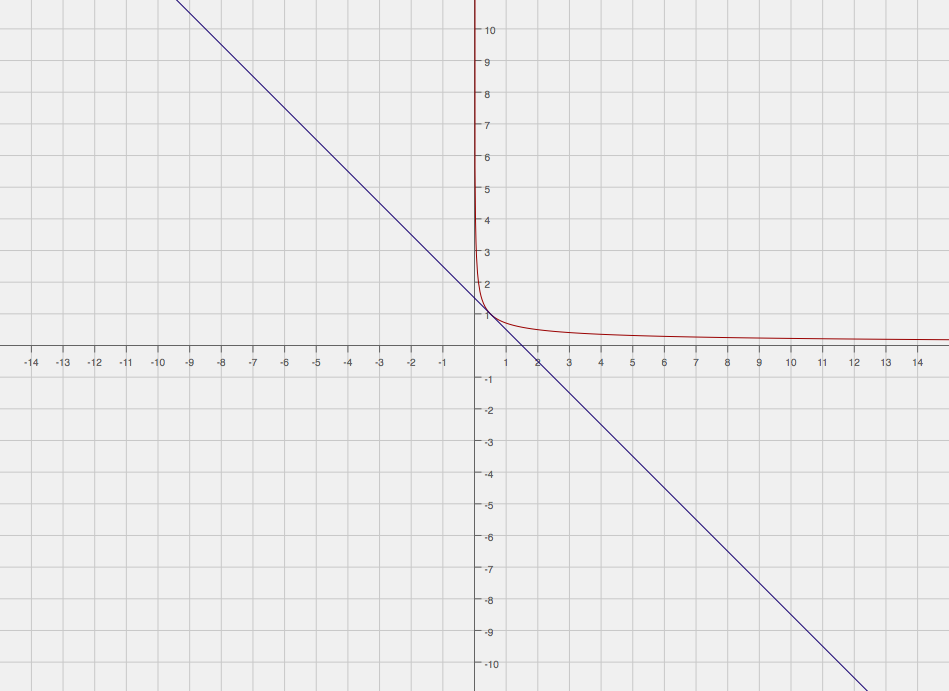
enter image source here

Hopefully this helps!