Question

How did earlier mathematicians calculate limits so accurately?

Especially things like how `lim_(x->0)` `(sinx^@/x^@)=sin1` but `lim_(x->0)` `(sinx^"rad"/x^"rad")=1`

Answer 1

With the exception of using L'Hospital's Rule and Taylor Series (which both rely on Calculus) they would use the same techniques that we currently use.

Most notably is that the limit you have used as an example, which can easily be derived using basic geometry.

Example

This is a technique used by Archimedes circa 250BC where he used regular polygons inside and outside to obtain approximations for `pi`. I quite like this example as it shows the brilliance of the early mathematicians centuries before modern mathematics.

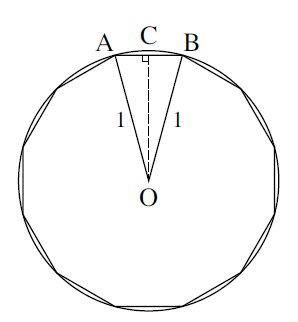
The above figure shows a regular `12`-sided polygon inscribed in a circle of radius `1` unit, centre `O`, `AB` is one of the sides of the polygon. `C` is the midpoint of `AB`. Archimedes used the fact that the circumference of the circle is greater that the perimeter of this polygon.

Now,

`360^o div 12 = 30^o => hat(AOB) = 30^o`
`C` is the midpoint of `AB => AB=2BC`
`:. COB =15^o`

By trigonometry we have:

`sin hat(COB)=(BC)/1`
But `AB=2BC` and `hat(COB)=15^o => sin 15^'=1/2AB`
`:. AB = 2sin15^o`

Using `cos2A -= 1-2sin^2A` we have:

`cos 30^o = 1-2sin^2 15^o`
`:. sqrt(3)/2 = 1-2sin^2 15^o`
`:. 2sin^2 15^o = 1-sqrt(3)/2`
`:. sin^2 15^o = (1-sqrt(3)/2)/2`
`:. sin^2 15^o = (2-sqrt(3))/4`
`:. sin 15^o = 1/2sqrt(2-sqrt(3)`

Then he calculated the perimeter of the polygon using:

`P = 12AB`
`\ \ \ = 24sin 15^o`
`\ \ \ = 12 sqrt(2-sqrt(3)`

Then as above:

Circumference of circle `gt` perimeter of polygon
`:. (2pi)(1) gt 12 sqrt(2-sqrt(3)`
`:. pi gt 6 sqrt(2-sqrt(3)` ..... [A]

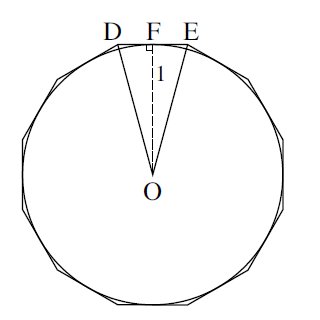
Next Archimedes considered a 12-sided polygon that lies outside a circle of radius `1` unit, which touches each side of the polygon. `F` is the midpoint of `DE`. Archimedes used the fact that the circumference of the circle is less that the perimeter of this polygon.

As before,

`hat(DOE) = 30^o => hat(FOE)=15^o`
And, `DE=2FE`

By trigonometry:

`tan hat(FOE)=(FE)/1`
But `DE=2FE` and `hat(FOE)=15^o => tan15^o=1/2 \ DE`

Using `tan(A+B)=(tanA+tanB)/(1-tanAtanB)` we have:

`tan 30^o = (2tan15^o)/(1-tan^2 15^o)`
`:. 1/sqrt(3) = (2t)/(1-t^2)`, where `t=tan 15^o`
`:. 2sqrt(3)t = 1-t^2`
`:. t^2+2sqrt(3)t-1 = 0`

This is quadratic in `t(=tan15^o)`, and so using the quadratic formula:

`t = (-2sqrt(3) +- sqrt(2sqrt()^2-4(1)(-1)) ) /2`
`\ \ = -sqrt(3) +- 2`
But as `t=tan 15^o > 0 => tan 15^o = 2-sqrt(3)`

And so the perimeter of this polygon is:

`P = 12 DE`
`\ \ \ = 12 tan 15^o`
`\ \ \ = 24(2-sqrt(3))`

This time:

Circumference of circle `lt` perimeter of polygon
`:. (2pi)(1) lt 24(2-sqrt(3))`
`:. pi lt 12(2-sqrt(3))` ..... [B}

Combining the results [A] and [B} Archimedes then showed that:

`6 sqrt(2-sqrt(3)) lt pi lt 12(2-sqrt(3))`
`:. 3.10582 ... lt pi lt 3.21539 ...`
`:. 3.106 lt pi lt 3.215`

And of course we know that:

`3.141592653589793238462 ...`

Archimedes used this same technique on a `24`-sided polygon, and finally `48`- and `96`-sided polygons. Those early Greek philosophers sure did now their stuff !

As we take larger and larger `n`-sided polygons, this is the equivalent of the limiting process. Remember this was several hundred years before Isaac Newton, and Leibniz started using limits of infinitesimals for early Calculus in the 17th Century.