Question

What is the area inside the polar curve `r=1`, but outside the polar curve `r=2costheta`?

Answer 1

`A = pi/3 + sqrt(3)/2 ~~ 1.9132`

Explanation:

Here is the graph of the two curves. The shaded area, `A`, is the area of interest:

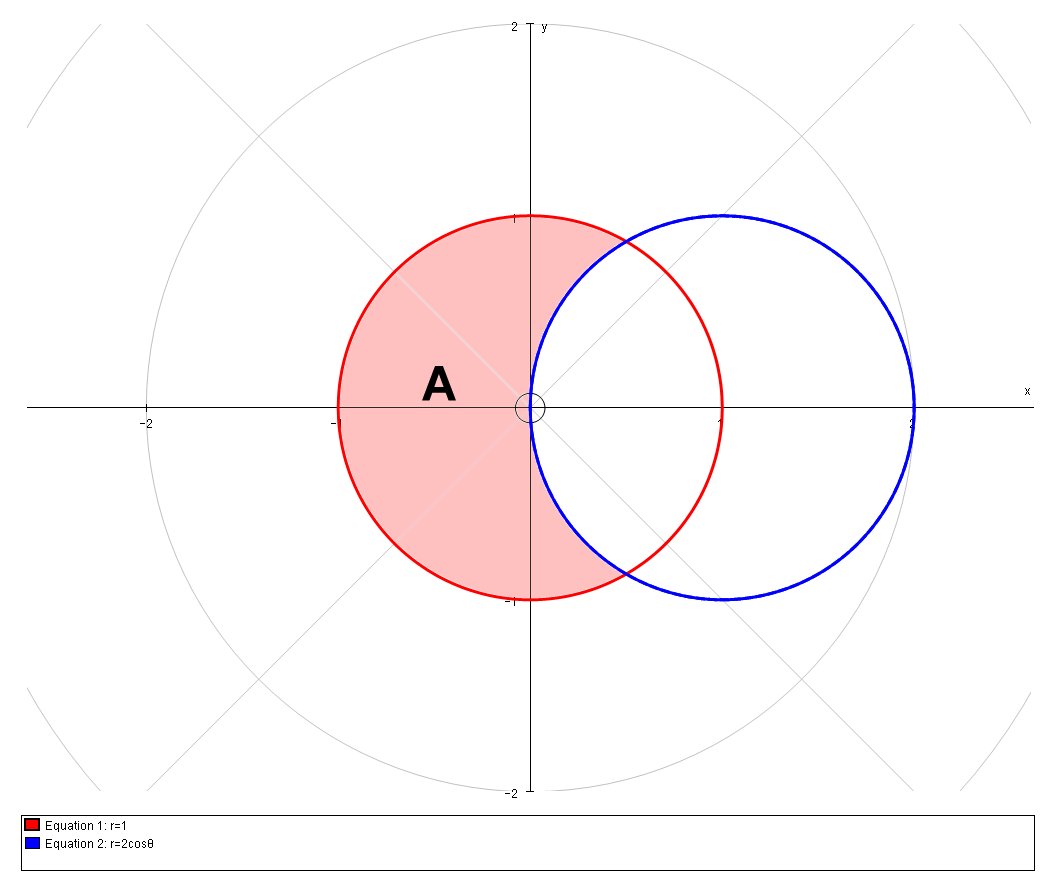
This is a symmetrical problems so we only need find the shaded area, `B` and subtract twice this from that of a unit circle (`r=1`).

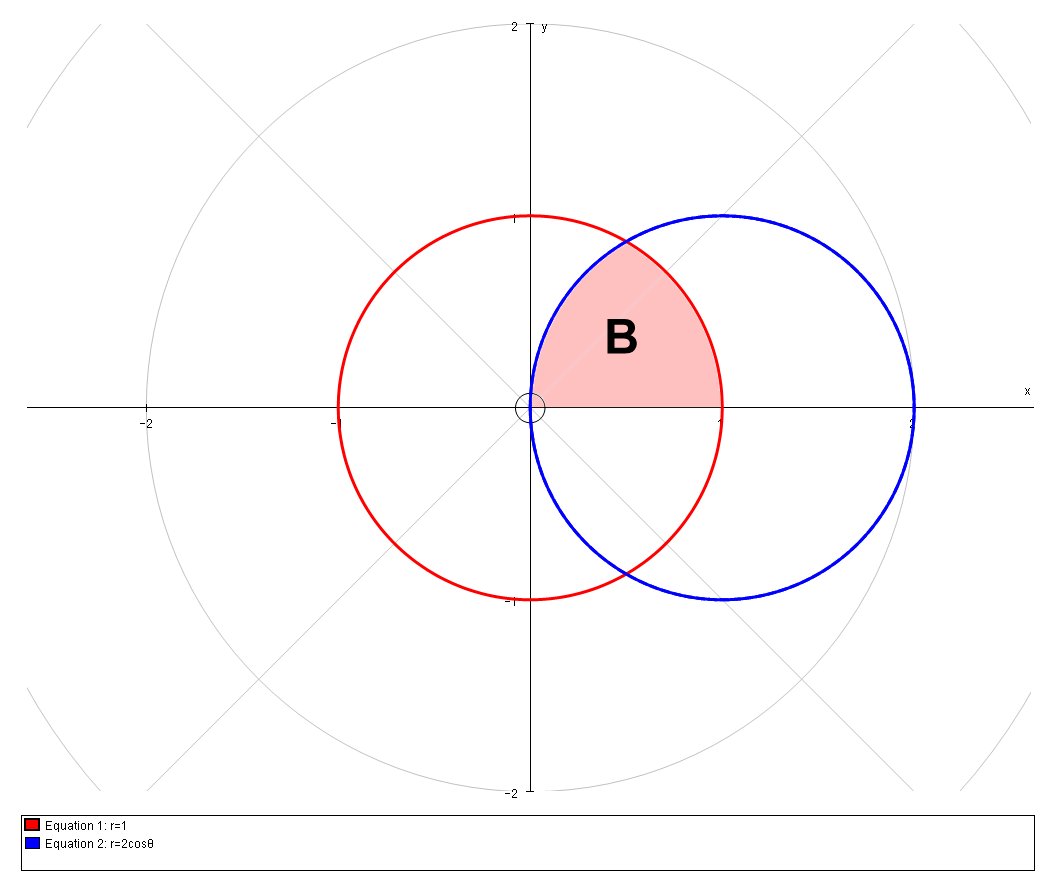
We can find the polar coordinate of the point of intersection in Q1 by simultaneously solving the polar equations:

`r=2cos theta`
`r=1`

From which we get:

`2cos theta = 1 =>cos theta = 1/2`
`:. theta = pi/3`

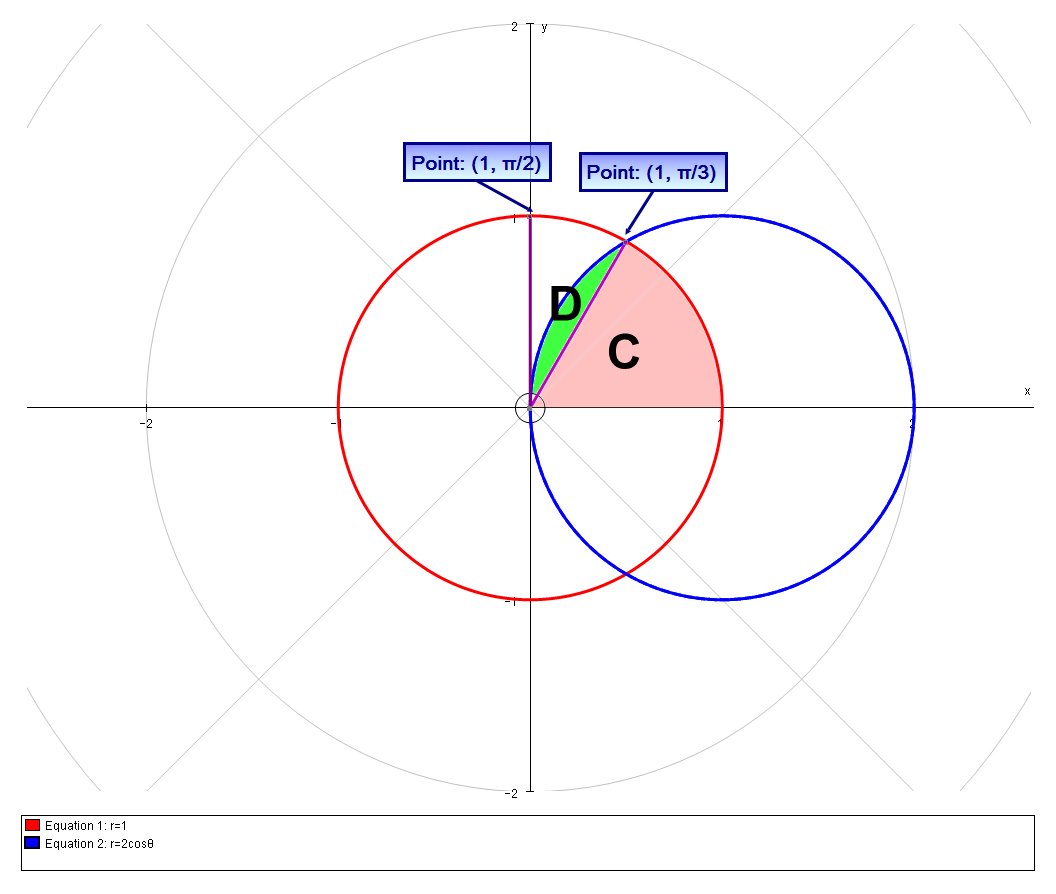
So we can easily calculate the area, `B`, which is that of the a circle sector `C` and that bounded by the curve `r=2costheta` where `theta in (pi/3,pi/2)`

The area, `C` is simply `1/2r^2theta`:

`A_C = 1/2 * 1 * pi/3`
`\ \ \ \ \ = pi/6`

And we calculate the area of the segment `B`, via Calculus using:

`A = int \ 1/2r^2 \ d theta`

Thus:

`A_D = int_(pi/3)^(pi/2) \ 1/2(2costheta)^2 \ d theta`
`\ \ \ \ \ = int_(pi/3)^(pi/2) \ 1/2 \ 4cos^2 theta \ d theta`
`\ \ \ \ \ = 2int_(pi/3)^(pi/2) \ cos^2 theta \ d theta`
`\ \ \ \ \ = 2int_(pi/3)^(pi/2) \ 1/2(cos2theta+1) \ d theta`
`\ \ \ \ \ = int_(pi/3)^(pi/2) \ cos2theta+1 \ d theta`
`\ \ \ \ \ = [1/2sin2theta + theta]_(pi/3)^(pi/2)`
`\ \ \ \ \ = (1/2sin(pi)+pi/2) - (1/2sin((2pi)/3)+pi/3)`
`\ \ \ \ \ = (0+pi/2) - (1/2 sqrt(3)/2+pi/3)`
`\ \ \ \ \ = pi/2 - sqrt(3)/4-pi/3`
`\ \ \ \ \ = pi/6 - sqrt(3)/4`

So then the total area we require, is given by:

`A_A = pi(1)^2 - 2(A_C+A_D)`
`\ \ \ \ \ = pi - 2(pi/6 + pi/6 - sqrt(3)/4)`
`\ \ \ \ \ = pi - 2(pi/3 - sqrt(3)/4)`
`\ \ \ \ \ = pi - (2pi)/3 + (2sqrt(3))/4`

`\ \ \ \ \ = pi/3 + sqrt(3)/2`