Question

How do you identity if the equation `x^2-y^2+8x=16` is a parabola, circle, ellipse, or hyperbola and how do you graph it?

Answer 1

The given equation fits the general Cartesian form of a conic section:

`Ax^2+Bxy+Cy^2+Dx+Ey+F = 0`

where `A = 1, B=0, C = -1, D=8, E = 0, and F = -16`

In the section entitled, Discriminant, the reference tells us to compute `B^2-4(A)(C)`:

`0^2-4(1)(-1) = 4`

The result is `> 0`, therefore, is it a hyperbola. Furthermore, `A+C = 1-1 = 0`, therefore, it is a rectangular hyperbola.

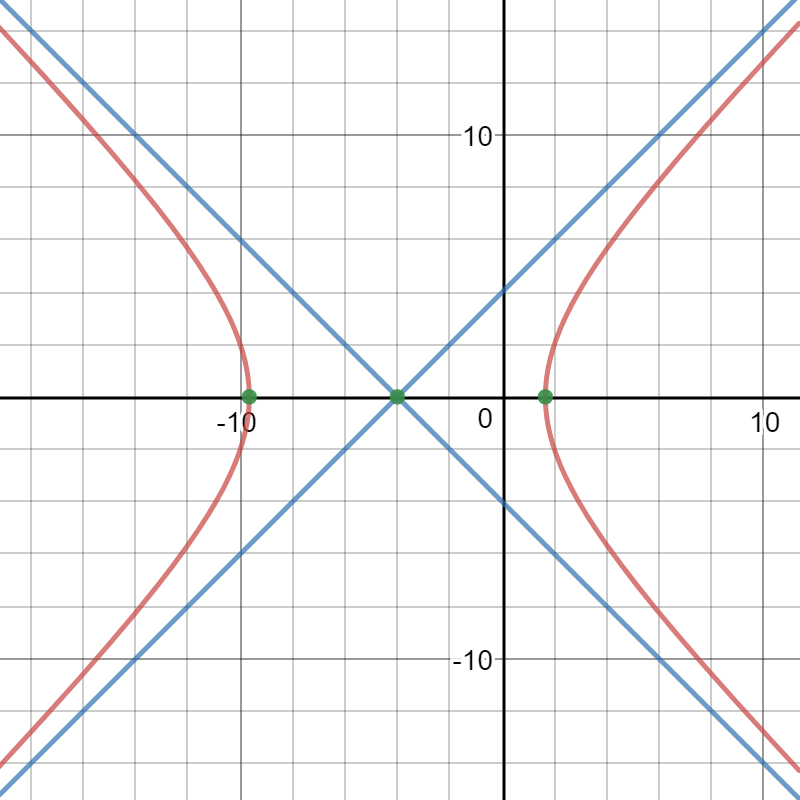
To graph the hyperbola, I recommend that you write the equation in a form that gives you, the center, the vertices and the equations of the asymptotes:

`(x^2-h)^2/a^2-(y-k)^2/b^2=1`

center: `(h,k)`
vertices: `(h-a,k)` and `(h+a,k)`
asymptotes: `y = -b/a(x-h)+k` and `y = b/a(x-h)+k`

Let's work on that form.

Add `h^2` to both sides of the equation:

`x^2+8x+h^2-y^2=16+h^2`

The expansion of the pattern `(x-h)^2=x^2-2hx+h^2` tells us that the following equation will allow us to find the value of h:

`-2hx = 8x`

`h = -4`

The absence of a y term tells us that `k = 0`

Substitute the left side of the pattern into the equation:

`(x-h)^2-(y-k)^2=16+h^2`

Substitute the values for h and k into the equation:

`(x-(-4))^2-(y-0)^2=16+(-4)^2`

Simplify

`(x-(-4))^2-(y-0)^2=32`

Divide both sides by 32:

`(x-(-4))^2/32-(y-0)^2/32=1`

Write the denominators as squares:

`(x-(-4))^2/(4sqrt2)^2-(y-0)^2/(4sqrt2)^2=1`

The center is `(-4,0)`

The vertices `(-4-4sqrt2,0)` and `(-4+4sqrt2,0)`

The equation of the asymptotes are:

`y = -b/a(x-h) + k` and `y = b/a(x-h)+k`

`y = -(x- (-4))` and `y = (x- (-4))`

`y = -x-4` and `y = x+4`

Here is a graph with the equation, the center, the vertices and the asymptotes: