Question

Question #7c02d

Answer 1

(b) `2.5` `"m/s"^2` upward

Explanation:

We're asked to calculate the acceleration of the lift, given what a balance indicates the weight of a `20`-`"kg"` object is.

I'll answer this without the use of a free-body diagram, and rather use more conceptual understanding... (it's always good to draw a free-body diagram when solving dynamics problems, though!).

The true weight `w` of the object is

`w = mg = (20color(white)(l)"kg")(9.81color(white)(l)"m/s"^2) = color(red)(196.2` `color(red)("N"` `~~ 200` `"N"` (`1` significant figure)

The spring balance, however, indicates its weight as `250` `"N"`. What does this mean?

You may have felt a sensation in a lift/elevator before where you seem to weight more than you actually do. This happens when the lift/elevator's acceleration is upward, because while it's accelerating upward, you appear to push down on the elevator's floor with more force.

Therefore, the acceleration of the lift must be upward, since the `20`-`"kg"` object apparently weighs more.

Since the acceleration is directed upward, the net force must also be directed upward, so the net force acting on the lift is

`sumF_y = 250` `"N"` `- 200` `"N"` `= color(green)(50` `color(green)("N"` upward

The acceleration is thus

`a_y = (sumF_y)/m = color(green)(50color(white)(l)color(green)("N"))/(20color(white)(l)"kg") = color(blue)(2.5` `color(blue)("m/s"^2` upward

Thus option (b) is correct.

Answer 2

b)

Explanation:

If the lift was not in movement `F= mg = 20 kg xx 10 m/s^2 = 200 N` Therefore there is a new force toward down of 50 N due to the acceleration of the lift upwards
`(F = ma`
`a = F/m = (50 N)/(20 kg )= 2,5 m/(s^2))`

Answer 3

B

Explanation:

Before we start, we list out all the given information:
`m=20"kg"`
`N=250"N"`

Reading on a weight scale is not to the normal/reaction force, `N`.

Newton's first law states that an object will remain its motion (stay at rest or continue moving at constant velocity if moving) there is no external force acting on it.
Newton's second law states that the motion of an object is directly proportional to the sum of motive forces.
Thus, `SigmaF=ma` or `F_"net"=ma`

When the lift (elevator) is at stationary, the only force acting on it is Gravity. An object, in this case, a mass of `20`kg will be experiencing a force acting on it. The force due to gravity is weight, `W=mg` where `g` is the gravitational acceleration.

`:.F_"net"=N-mg=0`
`N=mg`

But now, the lift is accelerating.

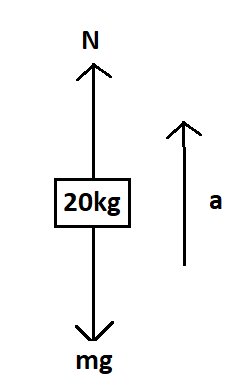
[I assume the elevator is moving up]

`F_"net"=ma=20a`
[that's why i put positve a and it makes things easier]

`F_"net"=N-mg`
`20a=250-20*10`
[I use `g="10"ms^-2` as i noticed all the options are factors of 5]
`a=50/20`
`a=2.5"ms"^-2`

[You may assume the elevator is moving down, you will reach the same answer eventually as negative signs would be cancelled off]
`F_"net"=ma=-20a`
`-20a=250-20*10`
`a=-50/20`
`a=-2.5"ms"^-2`

moving downwards with `a=-2.5"ms"^-2`
`-a=-2.5"ms"^-2`
`a=-2.5"ms"^-2`

Acceleration is vector quantity: with both magnitude and direction

Negative sign means downward, positive means upward
[Assuming the object is at origin on a cartesian plane. Moving up you will get positive value and vice versa.]