Question

Question #fb349

Answer 1

Here's what I got.

Explanation:

As you know, we can use four quantum numbers to describe the position and spin of an electron in an atom.

I assume that you're fairly familiar with how they work, so I won't go into too much detail here.

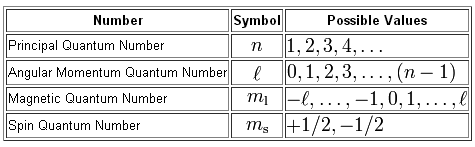
So, you know that you must find the sets of quantum numbers that can be used to describe an electron located in the `4d` subshell, i.e. in one of the `5` possible `4d` orbitals.

The number added in front of the subshell tells you the energy level on which the subshell is located, i.e. the value of the principal quantum number, `n`.

In your case, you have the `4d` subshell, so you can say that

`n = 4 ->` the fourth energy level

The `d` subshell is described by an angular momentum quantum number, `l`, that takes the value

`l = 2 ->` the d subshell

For the `d` subshell, the magnetic quantum number, `m_l`, can take one of five possible values

`m_l = {-2, -1, 0, 1, 2} ->` five orbitals in the d subshell

Each value of the magnetic quantum number describes one of the five orbitals present in the `d` subshell.

Finally, each orbital can hold a maximum of `2` electrons of opposite spins, which implies that the spin quantum number, `m_s`, can only take two possible values

`m_s = {-1/2, 1/2} ->` two electrons of opposite spins

So, you can say that the `4d` subshell can hold a maximum of

`5 color(red)(cancel(color(black)("orbitals"))) * ("2 e"^(-))/(1color(red)(cancel(color(black)("orbital")))) = "10 e"^(-)`

that can be described using the following sets of quantum numbers--each individual orbital is shown in a different color

• `n=4, l=2, color(blue)(m_l = -2), m_s = -1/2`
• `n=4, l=2, color(blue)(m_l = -2), m_s = +1/2`
• `n=4, l=2, color(purple)(m_l = -1), m_s = -1/2`
• `n=4, l=2, color(purple)(m_l = -1), m_s = +1/2`
• `n=4, l=2, color(red)(m_l = 0), m_s = -1/2`
• `n=4, l=2, color(red)(m_l = 0), m_s = +1/2`
• `n=4, l=2, color(darkgreen)(m_l = 1), m_s = -1/2`
• `n=4, l=2, color(darkgreen)(m_l = 1), m_s = +1/2`
• `n=4, l=2, color(darkorange)(m_l = 2), m_s = -1/2`
• `n=4, l=2, color(darkorange)(m_l = 2), m_s = +1/2`