How do you compute the volume of the solid formed by revolving the given the region bounded by #y=sqrtx, y=2, x=0# revolved about (a) the y-axis; (b) x=4?
2 Answers
I have chosen to do both parts by both shells and washers(discs). Therefore I have provided separate answers for questions (a) and (b). Here is part (b)
Explanation:
Part (b) by shells
For shells we'll take a slice parallel to the axis of rotation. SO that's a vertical slice at some value of
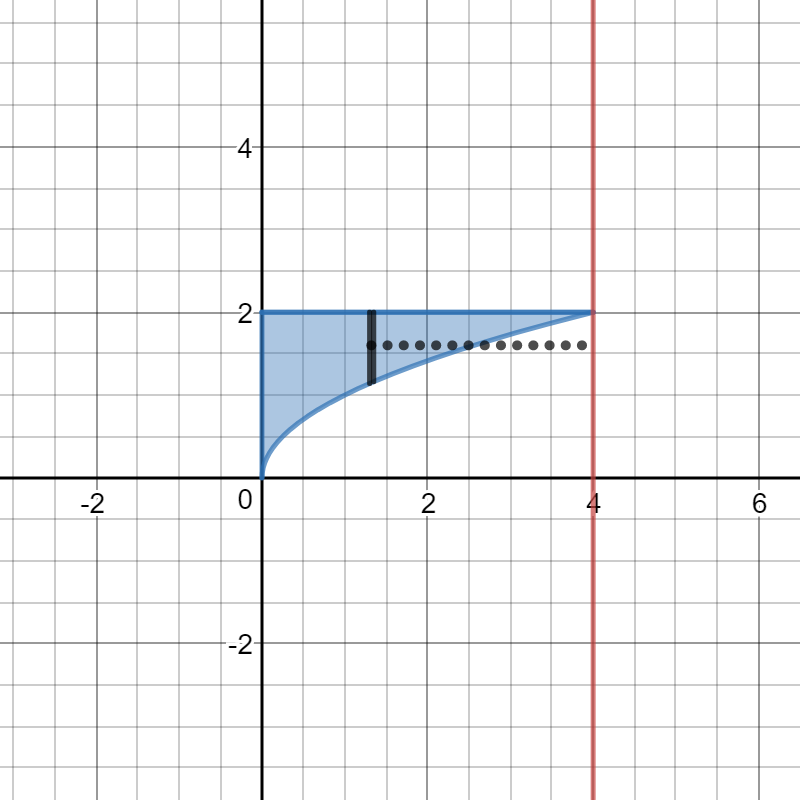
The radius of revolution is the distance between the slice and the axis of rotation. So,
As in part (a), the height is
The representative shell has volume
The volume of the resulting solid is
(Details are left to the reader.)
Part (b) by washers
Take the slice perpendicular to the axis of rotation. So we are taking a horizontal slice at a value of
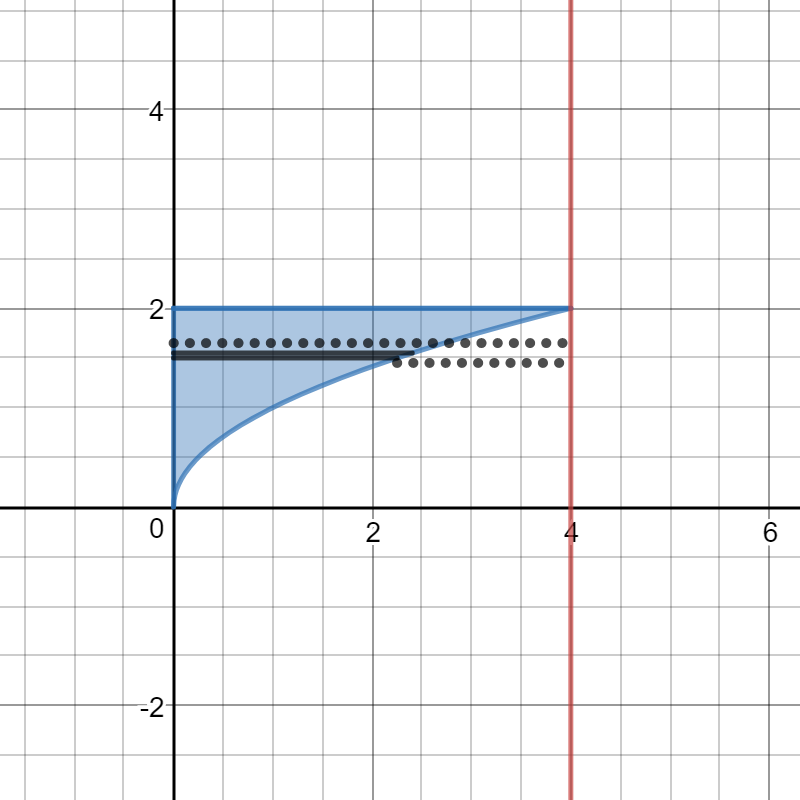
The revolution results not in a disc, but in a washer.
The outer (greater) radius is
The representative washer has volume
(Details are left to the reader.)
I have chosen to do both parts by both shells and washers(discs). Therefore I have provided separate answers for questions (a) and (b). Here is part (a)
Explanation:
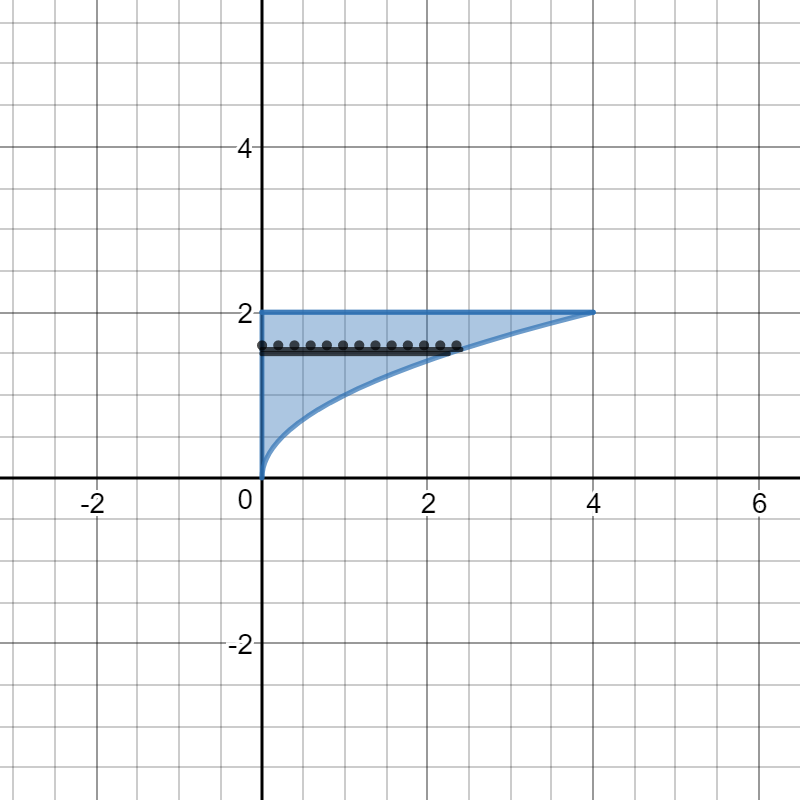
Here is a graph of the region:
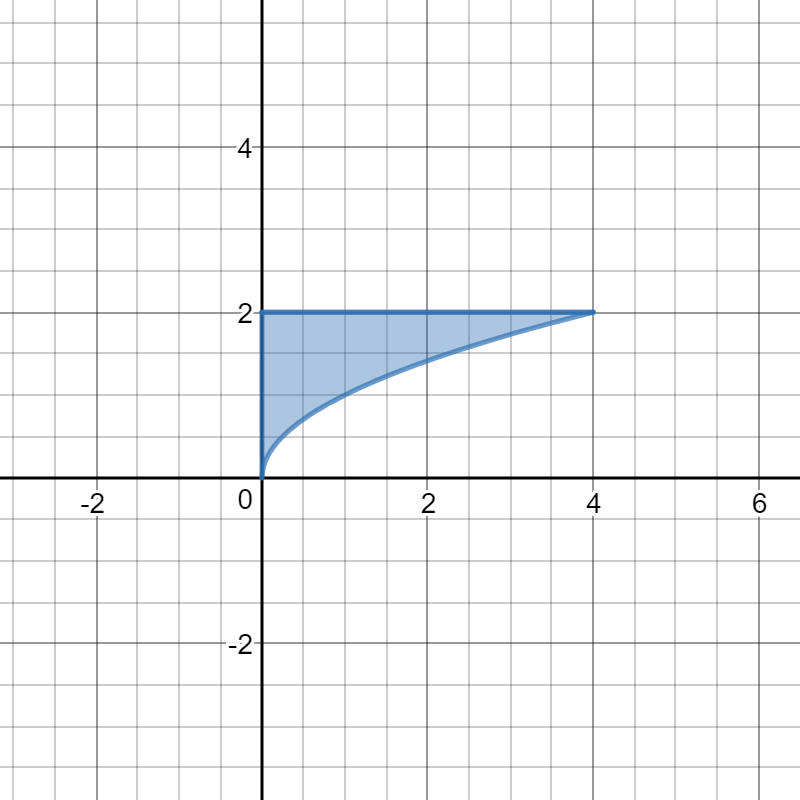
Part (a)
By Cylindrical Shells
We'll take a thin slice parallel to the axis of rotation -- in this case the
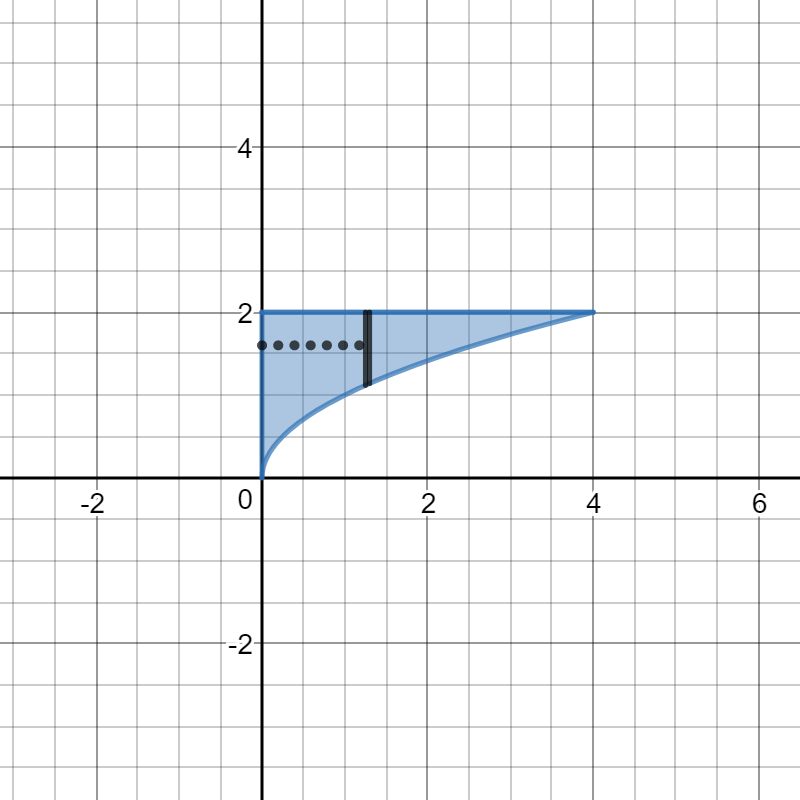
The location of the slice is
The volume of the representative shell is
In this case
So the representative shell has volume
The value of
(Details are left to the reader.)
Part (a) By discs (washers)
For discs or washers we take our slice perpendicular to the axiz of rotation.
In this case the thickness of the slice will be
The volume of the representative disc is
In this case
The volume of the representative disc is
The volume of the solid is

