Question

Question #22e71

Answer 1

Please see below.

Explanation:

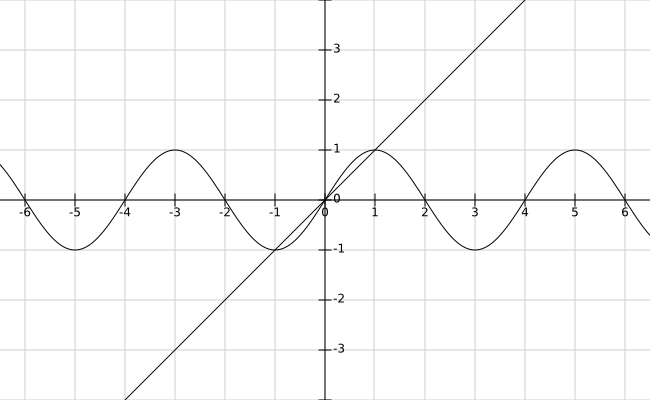
Find the points of intersection:

`sin((pix)/2) = x`

There isn't a nice algorithmic approach to solving this. A bit of experimenting (trial and error) will eventually reveal that `x = 0` is a solution. And so are `x=+-1`

Looking at a sketch of the graph should convince us that there are no other solutions.
For one thing, there cannot be any solutions outside the range of sine, which is `[-1,1]`

On `[0,1]` we have `sin((pix)/2) > x`

To see this, we might test at `x = 1/2` `sin(pi/4)= sqrt2/2 > 1/2`.

If the inequality were to be reversed, there would have to be a zero between. (Intermediate Value Theorem.)

In fact the inequality does go the other way on `[-1,0]`. That is

On `[-1,0]` we have `sin((pix)/2) < x`

By symmetry, it suffices to find the area on `[0,1]` and multiply by `2`.

So find `int_0^1 (sin((pix)/2)-x) dx = 2/pi-1/2`

The total are between the curves is `4/pi-1`

Answer 2

`A = (4-pi)/pi`

Explanation:

Consider the function:

`f(x) = sin((pix)/2)-x`

we have:

`f(0) = 0`

`f(1) = sin(pi/2) -1 = 0`

so the line joining the extremes of the graph of the function `f(x)`, that is the points `(0,0)` and `(1,0)` is the `x-`axis

Now evaluate:

`(d^2f)/(dx^2) = - pi^2/4 sinx < 0` for `x in(0,1)`

As the function is concave in the interval, its graph lays above the line joining the two extremes, which means:

`f(x) > 0` for `x in(0,1)`

The area comprised between the curves in this interval is then:

`A_+ = int_0^1 (sin((pix)/2)-x) dx = [-2/picos((pix)/2) -x^2/2]_0^1 = 2/pi-1/2 = (4-pi)/(2pi)`

For symmetry reasons the area comprised between the curves in the interval [-1,0] is the same:

`A_- = (4-pi)/(2pi)`

while externally to the interval the two graphs never cross as:

`abs x > 1`

`abs (sin((pix)/2) < 1`

Then the area comprised between the curves is:

`A= A_+ + A_- = (4-pi)/pi`