If the length of the Diagonal of a square is 10 inches. What is the length of each side?

Question

11109 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-25T17:00:31

Each side is #5sqrt2# or #7.071#

If the side od=f a square is #s#, the diagonal is #ssqrt2#.

This comes from Pythagoras as diagonal is

#sqrt(s^2+s^2)=sqrt(2s^2)=ssqrt2#

This is apparent from following figure

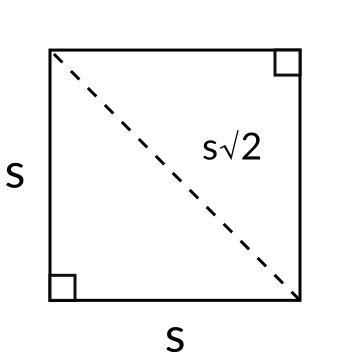
As such #ssqrt2=10#

and #s=10/sqrt2=(10xxsqrt2)/(sqrt2xxsqrt2)=(10xxsqrt2)/2=5sqrt2#

i.e. #5xx1.4142=7.071#

Answer 2 · 2017-07-25T17:06:02

#s = 5sqrt2" in"#

Let #d =# the length of the diagonal = #10" in"#
Let #s =# the length of the sides

Because the diagonal and two sides form a right triangle, we can use a variant of the Pythagorean Theorem:

#d^2 = s^2 + s^2#

Substitute 10 in for d:

#(10" in")^2 = s^2+s^2#

Combine like terms:

#(10" in")^2 = 2s^2#

Square the left side:

#100" in"^2 = 2s^2#

Divide both sides by 2:

#s^2 = 50" in"^2#

Use the square root operator on both sides:

#s = sqrt50" in"#

#s = 5sqrt2" in"#