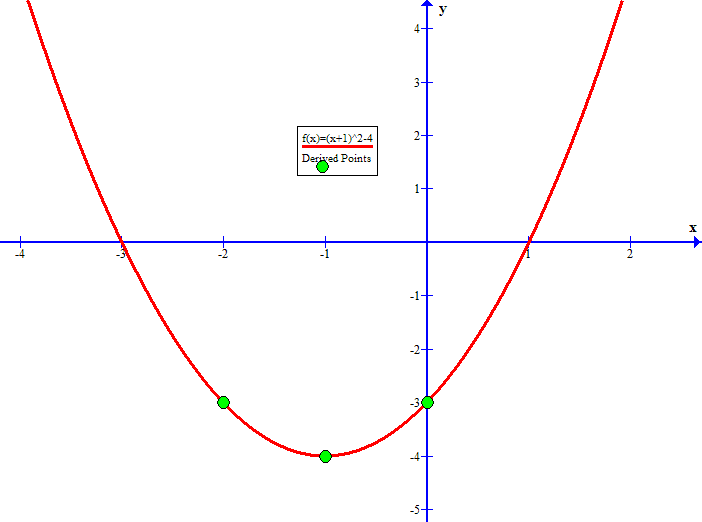
The general "vertex form" for a parabola (in standard position) is
#color(white)("XXX")y=color(green)m(x-color(red)a^2)+color(blue)b#
with vertex at #(color(red)a,color(blue)b)#
Notice that the given equation
#color(white)("XXX")y=(x+1)^2-4#
is almost in this form, and we could rewrite it as
#color(white)("XXX")y=color(green)1(x-color(red)(""(-1)))^2+color(blue)(""(-4))#
with vertex at #(color(red)(-1,color(blue)(-4)))#
The #y#-intercept is the value of #y# when #x=0#
and using the given equation:
#color(white)("XXX")y_(x=0) =(0+1)^2-4 =-3#
So #(0,-3)# is a point on the parabola.
Note that the axis of symmetry (for a parabola in standard position) is a vertical line (i.e. #x=# some constant) through the vertex;
so in this case the axis of symmetry is #x=color(red)(-1)#.
If the axis of symmetry is #x=-1# and #(0,-3)# is a point on the parabola,
since #(0,-3)# is a point #1# unit to the right of the vertical line #x=-1#
then there is another point #1# unit to the left of #x=-1# with the same #y# coordinate, namely #(-2,-3)#
The three points #(-1,-4), (0,-3), and (-2,-3)# should be sufficient to sketch the parabola (although, if you like, you could solve the given equation for the #x-intercept values as well by setting #y=0# in the original equation):