How do you find the remaining side of a 30^circ-60^circ-90^circ30∘−60∘−90∘ triangle if the side opposite 60^circ60∘ is 4?
1 Answer
Explanation:
A
The
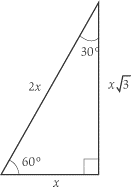 http://www.sparknotes.com/testprep/books/sat2/math1c/chapter6section2.rhtml
http://www.sparknotes.com/testprep/books/sat2/math1c/chapter6section2.rhtml
If the side opposite to
xsqrt 3 = 4x√3=4
x = 4/sqrt3x=4√3 ->→ divide both sides bysqrt3√3
x = 4/sqrt3 * color(red)(sqrt3/sqrt3)x=4√3⋅√3√3 ->→ rationalize the denominator by multiplying bysqrt3/sqrt3√3√3 , which is equal to11
x = (4sqrt3)/3x=4√33 ->→ multiply
Lastly, to find the side opposite to the
2x = 2 * (4sqrt3)/3 = (8sqrt3)/32x=2⋅4√33=8√33
So, the sides are

