How do you solve #ln(x)+e^x=0#?
2 Answers
I couldn't find it so I tried with a graphic method...
Explanation:
I tried to plot the right side as a function of
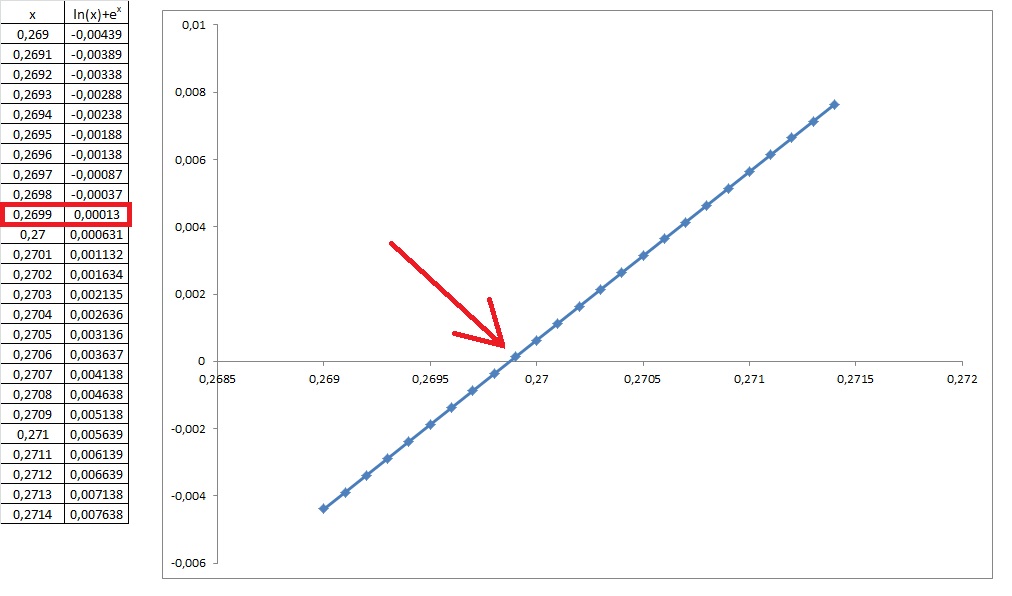
Explanation:
You will need to use a method such as Newton's to derive an approximation.
Beware: This answer will use Calculus
Newton's formula is used to find the roots of equations where algebra cannot be used successfully.
It states
#x_(n + 1) = x_n - f(x_n)/(f'(x_n))#
We start by finding a suitable starting value of
Then the derivative is given by
#f'(x) = 1/x + e^x#
If we use the initial approximation of
#f(x_1) = 0 + e = e#
#f'(x_1) = 1/1 + e = e +1#
The first approximation is given by
#x_(1 + 1) = 1 - e/(e + 1)#
#x_2 = 1 - e/(e + 1)#
This gives a result of

Hopefully this helps!


