Question

How to solve this problem?

Answer 1

Answer d is correct.

Explanation:

I would use identities.

We know that `sin^2x + cos^2x = 1`, then we have:

`(5/13)^2 + cos^2x = 1`

`cos^2x = 1 - 25/169`

`cos^2x = 144/169`

`cosx = +-12/13`

However, we know the answer must be negative because of the C-A-S-T rule, which is shown in the following picture.

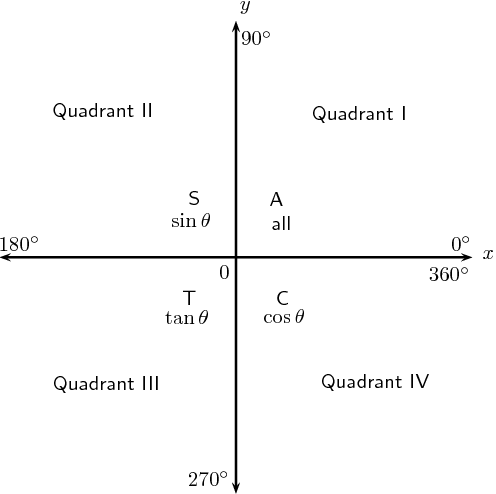
So only sine is positive on `pi/2 < x < pi` , which is equivalent to `90˚ < x <180˚`. So cosine will be `-12/13`.

Now we can use the quotient identity, which states that `tantheta = sintheta/costheta`. This stems from a right triangle with sides `x` and `y` and hypotenuse `r`. If `theta` is adjacent `x` and opposite `y`, then the ratios are

`costheta = x/r`
`sintheta = y/r`
`tantheta = y/x`

Now notice that

`(y/r)/(x/r) = y/x` or `sintheta/costheta = tantheta`

`tantheta = sintheta/costheta = (5/13)/(-12/13) = -5/12`

So answer d.

Hopefully this helps!

Answer 2

`"d)"` `- frac(5)(12)`

Explanation:

We know that `sin(theta) = frac(5)(13)`.

`sin(theta)` is also equal to `frac("opposite")("hypotenuse")`.

`Rightarrow frac("opposite")("hypotenuse") = frac(5)(13)`

So, the opposite and hypotenuse are equal to `5` and `13`, or they can be multiples of them.

For this problem, we can simply consider the opposite and hypotenuse to be `5` and `13`, respectively.

The hypotenuse of a triangle is its longest side.

Using Pythagoras' theorem:

`Rightarrow "opposite"^(2) + "adjacent"^(2) = "hypotenuse"^(2)`

`Rightarrow 5^(2) + "adjacent"^(2) = 13^(2)`

`Rightarrow "adjacent"^(2) = 13^(2) - 5^(2)`

`Rightarrow "adjacent"^(2) = 169 - 25`

`Rightarrow "adjacent"^(2) = 144`

`Rightarrow sqrt("adjacent"^(2)) = pm sqrt(144)`

`therefore "adjacent" = pm 12`

Now, `tan(theta)` is equal to `frac("opposite")("adjacent")`:

`Rightarrow tan(theta) = frac(5)(pm 12)`

The interval that we are provided with is `frac(pi)(2) < theta < pi`, i.e. the second quadrant.

In the second quadrant, all values of `tan(theta)` are negative.

So, `tan(theta)` cannot be equal to `frac(5)(+ 12) = frac(5)(12)`.

Therefore, `tan(theta)` is equal to `frac(5)(- 12) = - frac(5)(12)`.

In conclusion, the final answer is `"d)"` `- frac(5)(12)`.