Question

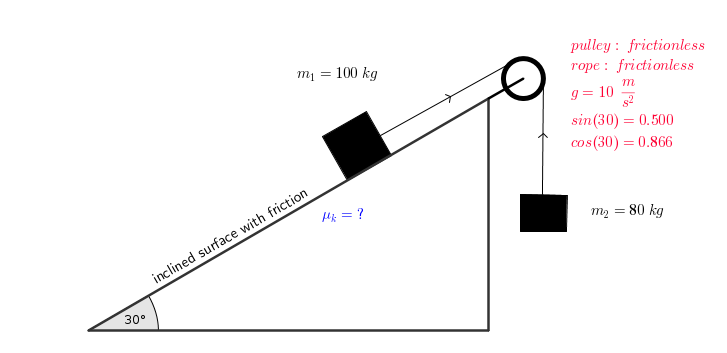
Due to friction ,the system as shown in the diagram remains motionless. Calculate the static coefficient of friction ?

Answer 1

`mu_s<=0.346`

Explanation:

Here's what I tried.

• I defined up the ramp as the positive direction.

Forces on `m_1`:

`sumF_x=T_1-(F_G)_x-f_s=0`

`sumF_y=n-(F_G)_y=0`

• `f_(s"max")=mu_sn`

• `(F_G)_x=m_1gsin(theta)`

• `(F_G)_y=m_2gcos(theta)`

• `n=mgcos(theta)`

I will refer to `f_(s"max")` simply as `f_s` from this point on, though I am still solving in terms of the maximum static friction.

`=>f_s=T_1-m_1gsin(theta)`

`=>mu_sm_1gcos(theta)=T_1-m_1gsin(theta)`

`=>color(darkblue)(mu_s=(T_1-m_1gsin(theta))/(m_1gcos(theta)))`

Forces on `m_2`:

`sumF=sumF_y=T_2-F_G=0`

• `F_G=m_2g`

Because we can assume a massless rope and frictionless pulley, `vecT_1` and `vecT_2` act as an "action/reaction" pair.

• `T_1=T_2=m_2g`

`=>mu_s=(m_2g-m_1gsin(theta))/(m_1gcos(theta))`

`=>mu_s=(cancel(g)(m_2-m_1sin(theta)))/(cancel(g)(m_1cos(theta))`

`=>color(darkblue)(mu_s=(m_2-m_1sin(theta))/(m_1cos(theta)))`

Using known values:

`mu_s=(80-100(0.500))/(100(0.866))`

`mu_(s"max")=0.346`

`=>mu_s<=0.346`