Question

A 1.0 kg object moving at 10 m/s 30° N of E collides centrally with a 2.0 kg object moving at 5 m/s 30° S of W. If the collision is inelastic, what is the velocity of the combined objects after collision?

If the collision is elastic, what is the velocity of each object after collision?

Answer 1

Inelastic: `0`

Elastic: `v_(1f)=-10"m"//"s, " v_(2f)=5"m"//"s"`

Explanation:

This problem can be solved using (2-D) momentum conservation.

Momentum is conserved in all collisions.

• In an inelastic collision, momentum is conserved as always, but energy is not; part of the kinetic energy is transformed into some other form of energy. For the first situation, we have an inelastic collision.

• The equation for momentum: `vecp=mvecv`

Momentum conservation:

`DeltavecP=0`

`=>color(darkblue)(vecP_f=vecP_i)`

We are given the following information:

• `|->m_1=1.0"kg"`
• `|->m_2=2.0"kg"`
• `|->v_(1i)=10"m"//"s"`
• `|->v_(2i)=5"m"//"s"`
• `|->theta_1=30^o`
• `|->theta_2=210^o`

Note that I am taking the positive x-axis to be my reference point for all angles.

Because we are given angles for the direction of the velocities of each of the masses, we will need to decompose the vectors into their parallel (x, horizontal) and perpendicular (y, vertical) components. Consequently, we will also have components of momentum.

`color(darkblue)(P_"net"=sqrt(P_x^2+P_y^2))`

Therefore, by momentum conservation, it should follow that:

`P_x=sump_x=p_(x1)+p_(x2)=m_1v_(1x)+m_2v_(2x)`

`P_y=sump_y=p_(y1)+p_(y2)=m_1v_(1y)+m_2v_(2y)`

Before and after the collision.

Diagram:

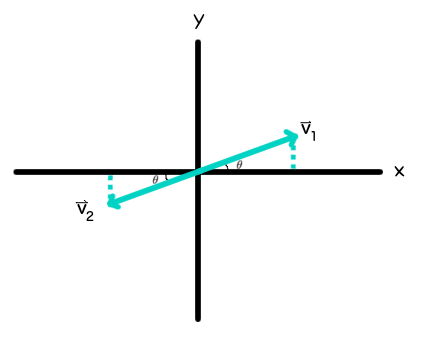
• This shows the paths that the masses would take if they continued in their initial direction.

We can begin by calculating the components of each of the velocities using basic trigonometry. I will demonstrate how this is done for one of the components below.

`sin(theta)="opposite"/"hypotenuse"`

`=>sin(theta_1)=v_(1y)/v_1`

`=>color(darkblue)(v_(1y)=v_1sin(theta_1))`

Similarly, we find:

• `color(darkblue)(v_(1x)=v_1cos(theta_1))`
• `color(darkblue)(v_(2x)=v_2cos(theta_2))`
• `color(darkblue)(v_(2y)=v_2sin(theta_2))`

We can now calculate the momentum before the collision.

`color(darkblue)(P_x=m_1v_(1x)+m_2v_(2x))`

`=>=m_1v_1cos(theta_1)+m_2v_2cos(theta_2)`

`=>=(1.0"kg")(10"m"//"s")cos(30^o)+(2.0"kg")(5"m"//"s")cos(210^o)`

`=>color(darkblue)(0)`

`color(darkblue)(P_y=m_1v_(1y)+m_2v_(2y))`

`=>=m_1v_1sin(theta_1)+m_2v_2sin(theta_2)`

`=>=(1.0"kg")(10"m"//"s")sin(30^o)+(2.0"kg")(5"m"//"s")sin(210^o)`

`=>color(darkblue)(0)`

`=>color(darkblue)(P_"net"=sqrt(0)=0)`

By momentum conservation, the momentum after the collision must also be `0`.

Therefore, after the collision, we have:

`P_f=m_1v_(f1)+m_2v_(f2)=0`

Because it is implied that the masses collide and stick together, they should have a common final velocity.

`=>m_1v_f+m_2v_f=0`

Submitting in our known masses, which do not change:

`=>v_f+2v_f=0`

`=>3v_f=0`

`:.v_f=0`

The final velocity of the masses is zero.

Note that this is, in fact, what is called a perfectly inelastic collision because the objects have a common final velocity.

`- - - - - --`

In an elastic collision, energy and momentum are both conserved, and the following equations can be derived using a combination of the two:

`color(darkblue)(v_(1f)=((m_1-m_2)/(m_1+m_2))v_(1i)+((2m_2)/(m_1+m_2))v_(2i))`

`color(darkblue)(v_(2f)=((2m_1)/(m_1+m_2))v_(1i)+((m_2-m_1)/(m_1+m_2))v_(2i))`

Using our known values, the parallel components of the final velocities are:

`v_(1fx)=((1.0"kg"-2.0"kg")/(1.0"kg"+2.0"kg"))(10cos(30^o)"m"//"s")+((2*2.0"kg")/(1.0"kg"+2.0"kg"))(5cos(210^o)"m"//"s")`

`=>v_(1fx)=(-(5sqrt3)/3-(20sqrt3)/9)"m"//"s"`

`=>v_(1fx)=-5sqrt3"m"//s"`

`=>color(darkblue)(~~-8.66"m"//"s")`

Similarly, `color(darkblue)(v_(2f)~~4.33"m"//"s")`

The perpendicular components of the final velocities are:

`v_(1fy)=((1.0"kg"-2.0"kg")/(1.0"kg"+2.0"kg"))(10sin(30^o)"m"//"s")+((2*2.0"kg")/(1.0"kg"+2.0"kg"))(5sin(210^o)"m"//"s")`

`=>v_(1fy)=(-10/6+10/3)"m"//"s"`

`=>color(darkblue)(v_(1fy)=-5"m"//"s")`

Similarly, `color(darkblue)(v_(2f)=2.5"m"//"s")`

We will now need to find the magnitude of each final velocity from the components.

`v_(1f)=sqrt(v_(1fx)^2+v_(1fy)^2)`

`=>=sqrt((8.66)^2+(-5)^2)`

`=>~~10"m"/"s"`

Similarly, `v_(2f)~~5"m"/"s"`

Since this is an elastic collision and we expect the balls to move off in the opposite direction that they approached each other from, we expect a negative velocity for `"m"_1` and a positive velocity for `"m"_2`.

Therefore:

• `v_(1f)=-10"m"//"s"`

• `v_(2f)=5"m"//"s"`

You can check the answer using momentum conservation. As calculated above, momentum before is `0`. Therefore, momentum after must also be `0`.

`P_f=m_1v_(1f)+m_2v_(2f)`

`=>(1.0"kg")(-10"m"//"s")+(2.0"kg")(5.0"m"//"s")`

`=>=0`