Question

Hey ,I am too much confused in taking the sign of g (means in equations like F=mg g should be eq ual to -9.8m/s2 or 9.8m/s2? Please answer with complete explanation..

Answer 1

This is a VERY complicated question because it involves the idea of VECTOR;

Explanation:

Acceleration is a vector so on top of having a numerical value (with units) it has also a DIRECTION; but what is direction?

Consider I scream: "look out, a car is approaching!!!", where do you run? It depends because the car could go towards you or away from you.

You see that direction is necessary and qualifies an important characteristic of some quantities such as velocity, force or acceleration (without it it would be difficult to qualify completely these quantities and be able to use them).

Our problem is `vecF=mveca`:
Here you see that Force and acceleration are vectors. When we do the calculations and decide for a positive direction we drop the arrow and use plus or minus in front of the values to indicate their directions.

What I suggest is to revise VECTORS first and then every time you have a problem involving forces (or any other vector quantity) first of all define a positive direction and refer to this for all your vector quantities.

So if one of your vectors, say acceleration, is pointing in the opposite direction to the positive one we will use a minus sign in front of its value to express this direction in all the formulae we use (you can appreciate that we need a way to discriminate between the two possibilities: acceleration in the same positive direction from acceleration in the opposite direction....plus or minus!):

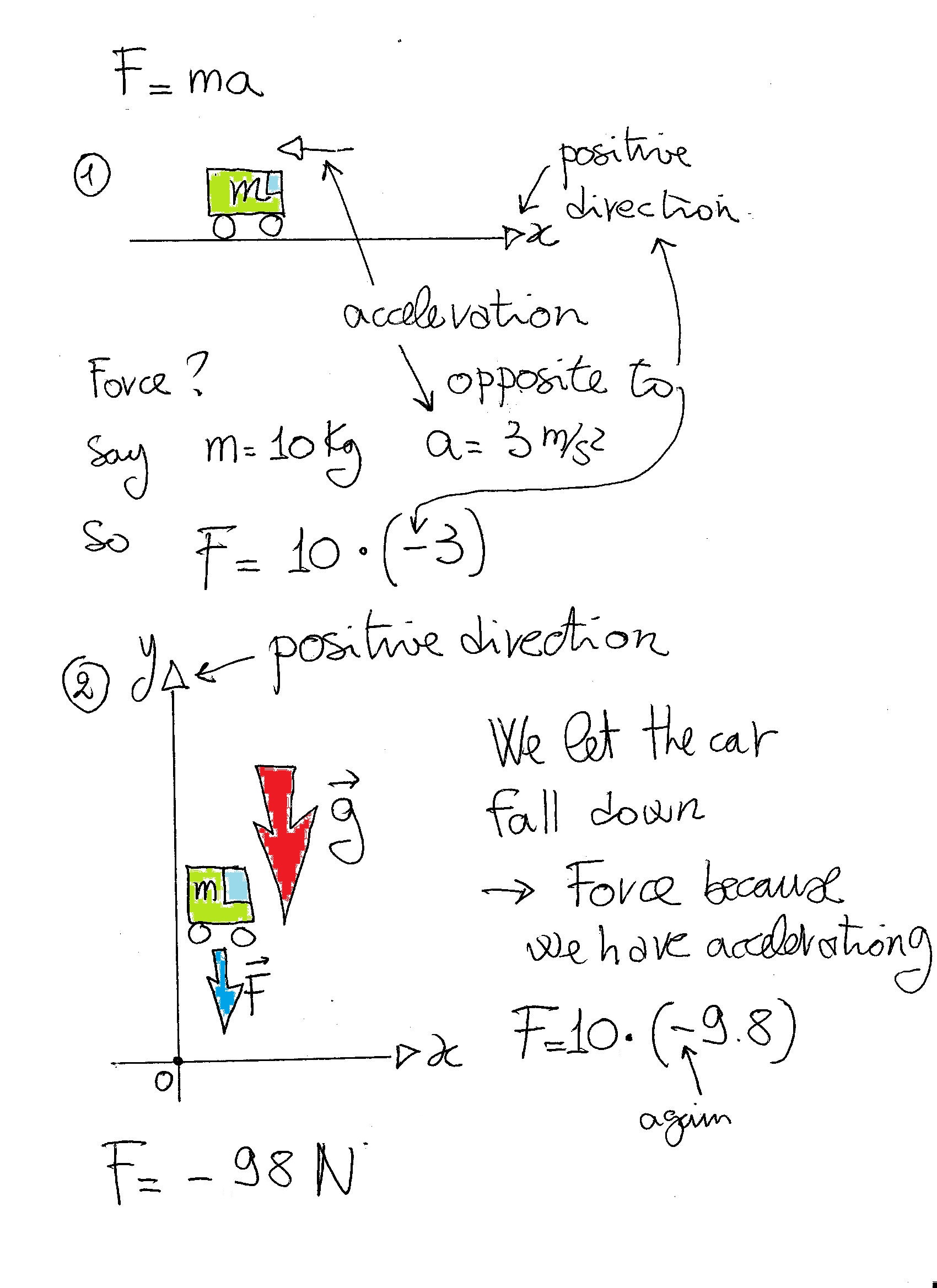
As you can see from the diagram the force (a vector) produced by a NEGATIVE (opposite to the positive direction) acceleration will retain the negative sign indicating that it will also be directed in the opposite direction from the positive one. helping us to understand its effect on the car.

Hope I didn't confuse you even more!

Answer 2

Very good answer above. I just wanted to throw out a quick tip for determining whether you should use `g` or `-g`.

Explanation:

• g is a constant, and is always positive, so any time you see “g” in an equation, use `9.81" m"//"s"^2`. So, for example, for gravitational potential energy `U_g=mgh`, you will always use `g=9.81"m"//"s"^2`.

• `-g` is the free-fall acceleration. If you are talking about the acceleration of an object, such as when using kinematics involving a projectile or falling object, it is always `-9.8"m"//s"^2` to indicate that the object is falling downward at a rate equal to `g`. What you really have is `a=-g=-(9.8"m"//"s"^2)`. So you would always put `-9.8"m"//"s"^2` into your kinematic equations for `a`.

You can use that above as a general rule so long as you remember that a downward force is negative and an upward force is positive (unless otherwise stated, but this is the convention).

So, for the force of gravity, you can write:

`F_g=mg`

where `g` is just `9.8"m"//s"^2`

And as long as you remember that the force of gravity points downward, you know that, as a force, it should be negative. The magnitude will always be positive regardless, so g is still used and not -g.