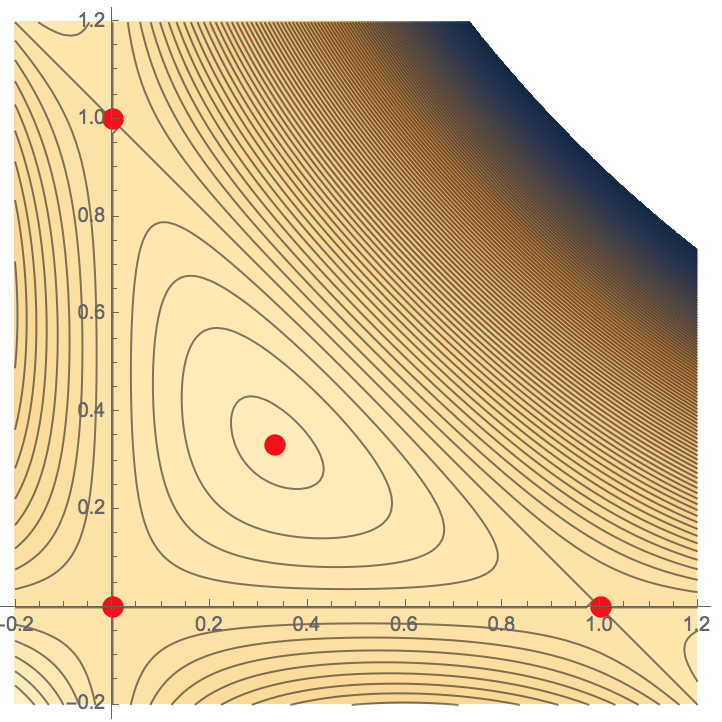
We can expand f to f(x,y)=xy-x^2y-xy^2. Next, find the partial derivatives and set them equal to zero.
\frac{\partial f}{\partial x}=y-2xy-y^2=y(1-2x-y)=0
\frac{\partial f}{\partial y}=x-x^2-2xy=x(1-x-2y)=0
Clearly, (x,y)=(0,0),(1,0), and (0,1) are solutions to this system, and so are critical points of f. The other solution can be found from the system 1-2x-y=0, 1-x-2y=0. Solving the first equation for y in terms of x gives y=1-2x, which can be plugged into the second equation to get 1-x-2(1-2x)=0 => -1+3x=0 =>x=1/3. From this, y=1-2(1/3)=1-2/3=1/3 as well.
To test the nature of these critical points, we find second derivatives:
\frac{\partial^{2}f}{\partial x^{2}}=-2y, \frac{\partial^{2}f}{\partial y^{2}}=-2x, and \frac{\partial^{2}f}{\partial x\partial y}=\frac{\partial^{2}f}{\partial y\partial x}=1-2x-2y.
The discriminant is therefore:
D=4xy-(1-2x-2y)^2
=4xy-(1-2x-2y-2x+4x^2+4xy-2y+4xy+4y^2)
=4x+4y-4x^2-4y^2-4xy-1
Plugging the first three critical points in gives:
D(0,0)=-1<0, D(1,0)=4-4-1=-1<0, and D(0,1)=4-4-1=-1<0, making these points saddle points.
Plugging in the last critical point gives D(1/3,1/3)=4/3+4/3-4/9-4/9-4/9-1=1/3>0. Also note that \frac{\partial^{2}f}{\partial x^{2}}(1/3,1/3)=-2/3<0. Therefore, (1/3,1/3) is a location of a local maximum value of f. You can check that the local maximum value itself is f(1/3,1/3)=1/27.
Below is a picture of the contour map (of level curves) of f (the curves where the output of f is constant), along with the 4 critical points of f.