The most straight forward way to resolve this particular is to get rid of the fraction as a first step.
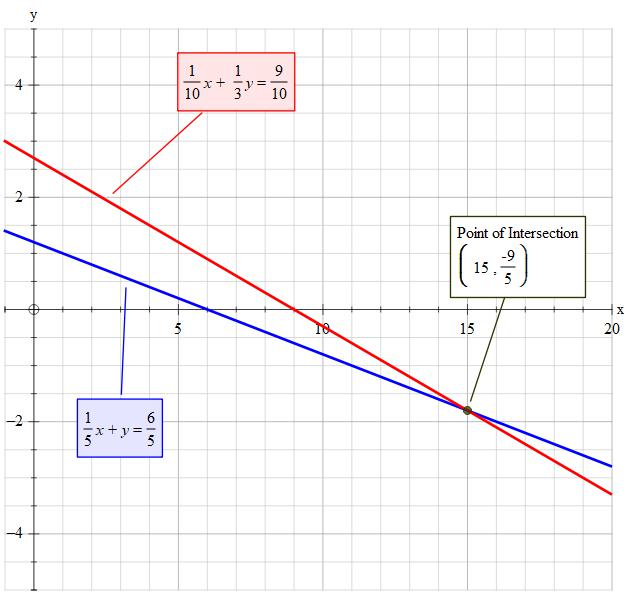
#1/5x+y=6/5" ".................Equation(1)#
#1/10x+1/3y=9/10" "..........Equation(2)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Consider Eqn(1)")#
#color(green)([x/5]color(white)("d")+color(white)("d")[ycolor(red)(xx1)]color(white)("d")=[6/5])#
#color(green)([x/5]color(white)("d")+color(white)("d")[ycolor(red)(xx5/5)]color(white)("d")=[6/5])#
#x/5+(5y)/5=6/5#
Multiply both sides by 5
#x+5y=6" "......................Equation(1_a)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Consider Eqn(2)")#
#color(green)([x/10color(red)(xx1)]+[y/3color(red)(xx1)]=[9/10color(red)(xx1)] )#
#color(green)([x/10color(red)(xx3/3)]+[y/3color(red)(xx10/10)]=[9/10color(red)(xx3/3)] )#
#(3x)/30+(10y)/30=27/30#
Multiply both sides by 30
#3x+10y=27" "...........Equation(2_a)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Putting it all together")#
#x+5y=6" "..................Eqn(1_a)#
#3x+10y=27" "............Eqn(2_a)#
#Eqn(2_a) -(3xxEqn(1_a))#
#3x+10y=27" "larr" "Eqn(2_a)#
#ul(3x+15y=18)" "larr" "3xxEqn(1_a)#
#0x-color(white)(2)5y=9#
Multiply both sides by (-1)
#+5y=-9#
Divide both sides by 5
#y=-9/5" ".............Eqn(3)#
I choose #Eqn(1_a)# it is works out more easily. You would still get the same answer if you used #Eqn(2_a)# but it would involve more work.
Using #Eqn(3)# substitute for #y# in #Eqn(1_a)#
#color(green)(x+5color(red)(y)=6" "->" "x+(5color(red)(xx-9/5))=6#
#x-9=6#
#x=6+9=15#