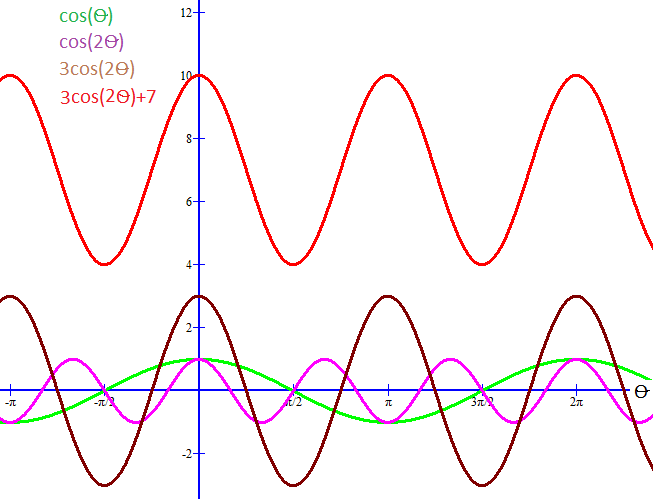
The standard cos function #color(green)(cos(gamma))# has a period of #2pi#
If we want a period of #pi# we need to replace #gamma# with something that will cover the domain "twice as fast" e.g. #2theta#.
That is #color(magenta)(cos(2theta))# will have a period of #pi#.
To get an amplitude of #3# we need to multiply all values in the Range generated by #color(magenta)(cos(2theta))# by #color(brown)3# giving
#color(white)("XXX")color(brown)(3cos(2theta))#
There is to be no horizontal shift, so the argument for #cos# will not be modified by any further addition/subtraction.
In order to achieve the vertical shift (that I assumed would be #color(red)(+7)# [substitute your own value]) we will need to add #color(red)7# to all values in our modified range:
#color(white)("XXX")color(red)(3 cos(2theta) +7)#