What is #int (8x)/e^(x^2) \ dx#?
2 Answers
Sep 26, 2017
I got:
Explanation:
Have a look:
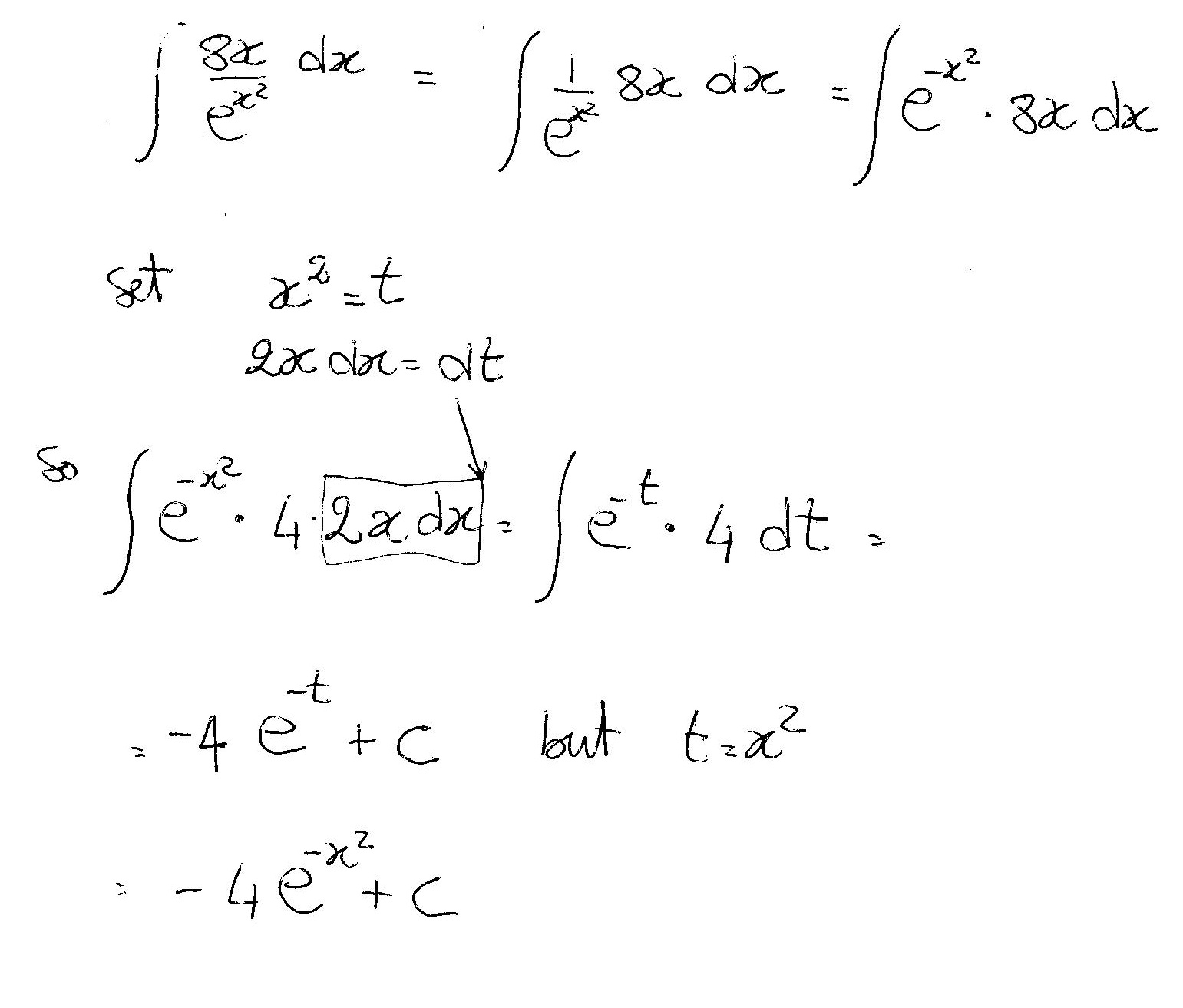
Sep 26, 2017
# int (8x)/e^(x^2) \ dx = -4 e^(-x^2) + c #
Explanation:
We seek:
# I = int (8x)/e^(x^2) \ dx #
Which we can write as:
# I = -4 \ int (-2x)e^(-x^2) \ dx #
With practice we can integrate this directly, but for the benefit of those unable to do this, let us perform substitution:
Let
#u=e^(-x^2) => (du)/dx = -2xe^(-x^2) #
So if we now substitute this into the integral, we get:
# I = -4 \ int \ du #
Which is now a standard integral, so we have:
# I = -4 u + c #
And reversing the substitution:
# I = -4 e^(-x^2) + c #


