Question

What are the extrema and saddle points of `f(x, y) = 6 sin(-x)* sin^2( y)` on the interval `x,y in[-pi,pi]` ?

Answer 1

Explanation:

We have:

`f(x,y) = 6sin(-x)sin^2(y)`
`\ \ \ \ \ \ \ \ \ \ \ = -6sinxsin^2y`

Step 1 - Find the Partial Derivatives

We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constant. Thus:

The First Derivatives are:

`f_x = -6cosxsin^2y`

`f_y = -6sinx(2sinycosy)`
`\ \ \ = -6sinxsin2y`

The Second Derivatives (quoted) are:

`f_(x x) = 6sinxsin^2y`

`f_(yy) = -6sinx(2cos2y)`
`\ \ \ \ \ = -12sinxcos2y`

The Second Partial Cross-Derivatives are:

`f_(xy) = -6cosxsin2y`

`f_(yx) = -6cosx(2sinycosy)`
`\ \ \ \ = -6cosxsin2y`

Note that the second partial cross derivatives are identical due to the continuity of `f(x,y)`.

Step 2 - Identify Critical Points

A critical point occurs at a simultaneous solution of

`f_x = f_y = 0 iff (partial f) / (partial x) = (partial f) / (partial y) = 0`

i.e, when:

# {: (f_x = -6cosxsin^2y, = 0, ... [A]), (f_y = -6sinxsin2y, = 0, ... [B]) :}}# simultaneously

Consider equation [A]

`-6cosxsin^2y = 0`

Then we have two solutions:

`cosx = 0 => x = +- pi/2`
`sin y = 0 => y = 0, +- pi`

Now let us use Eq[B] to find the corresponding coordinate:

`x = +-pi/2 => sin2y = 0`
`\ \ \ \ \ \ \ \ => 2y = +-pi, +- 2pi => y = +- pi/2, +-pi`

`y=0,+-pi => x in RR` (gutters)

Which gives us the following critical points:

`(+-pi/2, +-pi/2) \ \ \ \ \ \` (4 critical points)
`(+-pi/2, +-pi) \ \ \ \ \ \ \ \` (4 critical points)
`(alpha, 0) \ \ \ \ \ \AA alpha in RR \ \ \` (gutter line)
`(alpha, +-pi) \ AA alpha in RR \ \` (2 gutter lines)

Consider equation [B]

`-6sinxsin2y = 0`

Then we have two solutions:

`sinx \ \= 0 => x = 0,+- pi`
`sin2y = 0 => 2y = 0+- pi, +-2pi`
`\ \ \ \ \ \ \ \ => y = 0, +-pi/2, +- pi`

Now let us use Eq[A] to find the corresponding coordinate@

`x=0,+-pi => siny=0 => y=0,+-pi` (repeats of above)

`y=0 => x in RR` (repeat of above)

`y = +-pi/2 => cosx = 0`
`\ \ \ \ \ \ \ \ => x=+-pi/2` (repeats of above)

Which gives us no additional critical points:

Step 3 - Classify the critical points

In order to classify the critical points we perform a test similar to that of one variable calculus using the second partial derivatives and the Hessian Matrix.

`Delta = H f(x,y) = | ( f_(x x) \ \ f_(xy) ) , (f_(yx) \ \ f_(yy)) | = | ((partial^2 f) / (partial x^2),(partial^2 f) / (partial x partial y)), ((partial^2 f) / (partial y partial x), (partial^2 f) / (partial y^2)) | = f_(x x)f_(yy)-(f_(xy))^2`

Then depending upon the value of `Delta`:

`{: (Delta>0, "There is maximum if " f_(x x)<0),(, "and a minimum if " f_(x x)>0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :}`

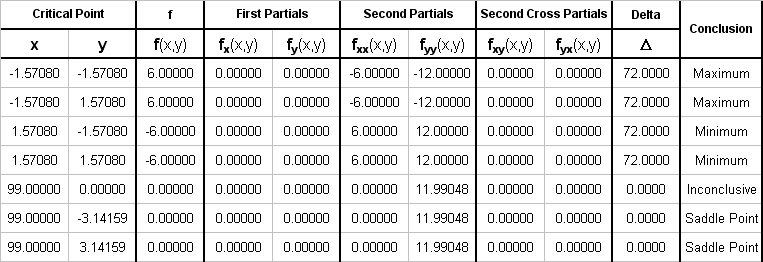
Using custom excel macros the function values along with the partial derivative values are computed as follows:

Here is a plot of the function

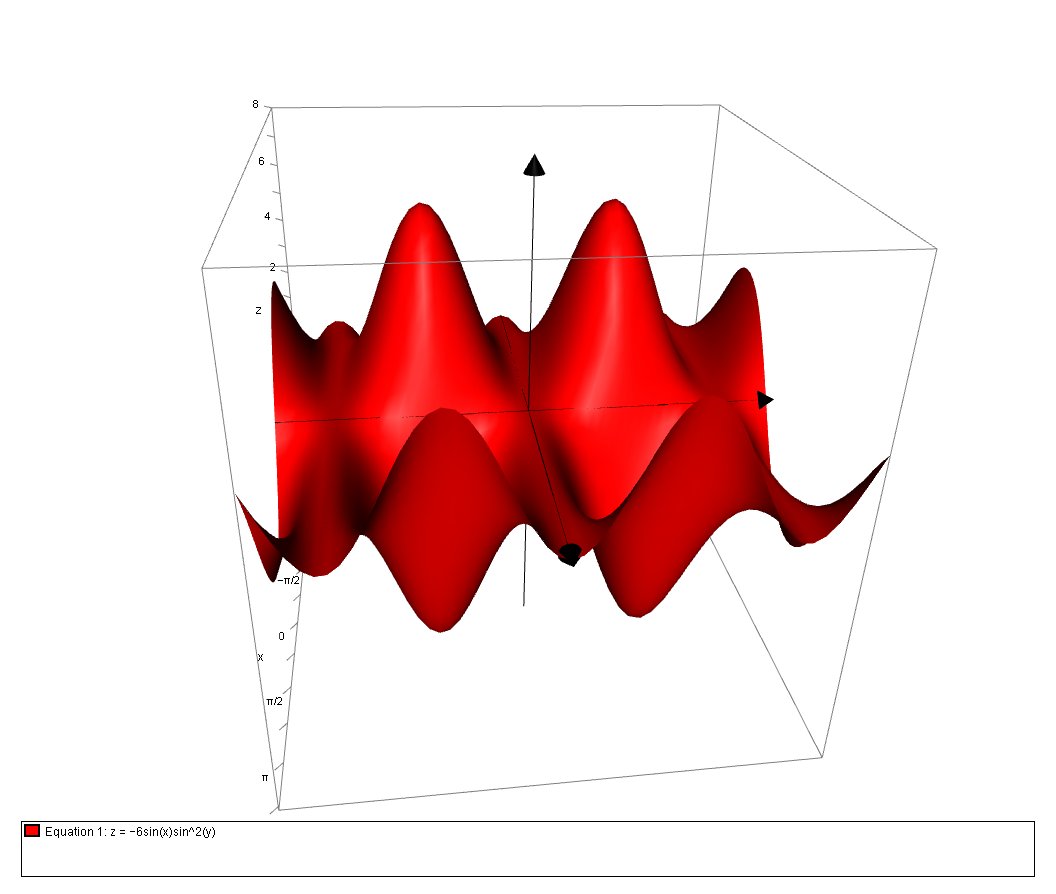
And the ploit with the critical points (and gutters)