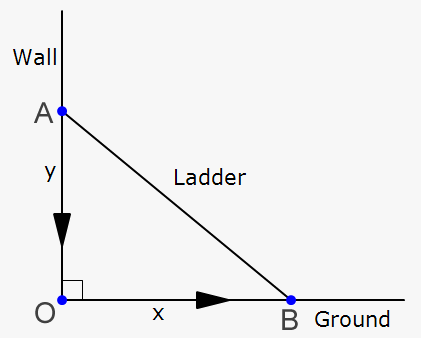
A ladder is leaning against a wall, and the floor and slipping. If the bottom of the ladder is slipping at #30 cms^(-1)# then how fast is the top of the ladder sliding down the wall when the ladder is at #45^o#?
1 Answer
It is sliding down at a rate (speed) of
Explanation:
Let us define the following variables:
# { (x, "Distance of bottom of ladder from the wall " (cms^-1)), (y, "Distance of top of ladder from the floor "(cm)), (t, "Time "(s)), (theta, "Angle between Ladder and floor "angle ABO " (radians)") :} #
We are told that
We aim to find
The ladder is a fixed length,
# x^2+y^2=l^2 #
Differentiating Implicitly wrt
# 2xdx/dt + 2ydy/dt=0 => xdx/dt + ydy/dt=0 #
# dx/dt = 30 => 30x + ydy/dt=0 #
# :. dy/dt = -30x/y # ..... [A]
Using trigonometry, we have:
# tan \ angle ABO = y/x => tantheta = y/x #
# theta = pi/4 => y/x=1 => x/y =1 #
With
# => dy/dt = -30 #
The minus sign denotes that the ladder is sliding down, i.e., the height