Question

What is the area enclosed by `r=theta^2cos(theta+pi/4)-sin(2theta-pi/12)` for `theta in [pi/12,pi]`?

Answer 1

The area is about 19.1849 by computational integration.

Explanation:

The area `S` enclosed by a polar curve `r=f(theta)` for `theta in [alpha,beta]` is obtained as follows.

`S=1/2int_alpha^beta{f(theta)}^2d` `theta`.

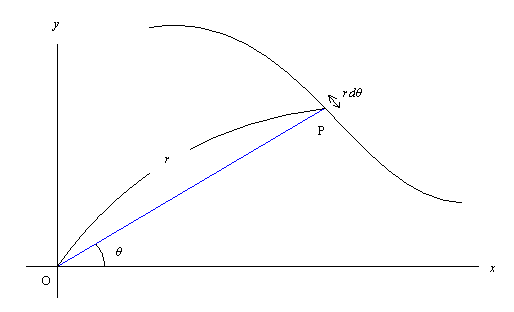
cited from a Japanese site, 極座標表示の場合の面積 http://www.geocities.jp/phaosmath/int1/polar.htm

Thus, the area in this question is:
`S=1/2int_(pi/12)^(pi){theta^2cos(theta+pi/4)-sin(2theta-pi/12)}^2d` `theta`.

This integration is so hard…
According to www.wolframalpha.com `S` is about 19.1849.
http://www.wolframalpha.com/input/?i=integrate+%7Bx%5E2cos(x%2Bpi%2F4)-sin(2x-pi%2F12)%7D%5E2%2F2+for+x%3D%7Bpi%2F12,pi%7D