How do you solve?
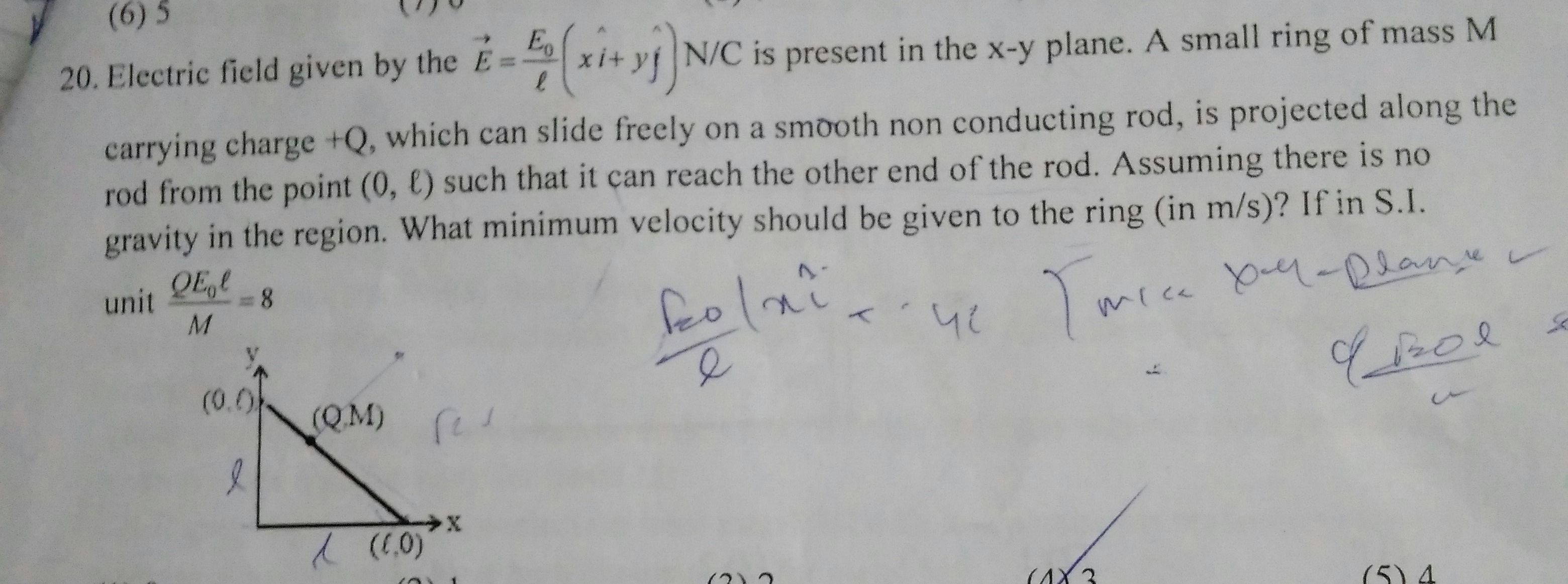
2 Answers
See below.
Explanation:
For a central field given by
where
It is given that the ring is projected along the rod from point
Electric force on charge
vecF=QvecE
We observe that at the initial point
From the foregoing we infer that initial kinetic energy given to the ring must be able to just pass the point
Work done by the charge to move a distance
dw=vec(F)*dvecs
Inserting given values and noting the negative slope of rod we get
dw=(QE_0)/l(xhat i+yhatj)cdot (dxhat i-dyhatj)=(QE_0)/l(xdx-ydy)
Total work done to reach point
w=int_0^(l/2) (QE_0)/lxdx-int_(l/2)^0 (QE_0)/lydy
=>w=(QE_0)/l(|x^2/2|_0^(l/2)+|y^2/2|_0^(l/2))
=>w=QE_0l/4
Equating work done with initial kinetic energy to be given to the mass we get
1/2Mv_min^2=QE_0l/4
=>v_min^2=(QE_0l)/(2M)
It is given that
v_min^2=8/2
:.v_min=2"ms"^-1

