What is the maximum value of the given function?
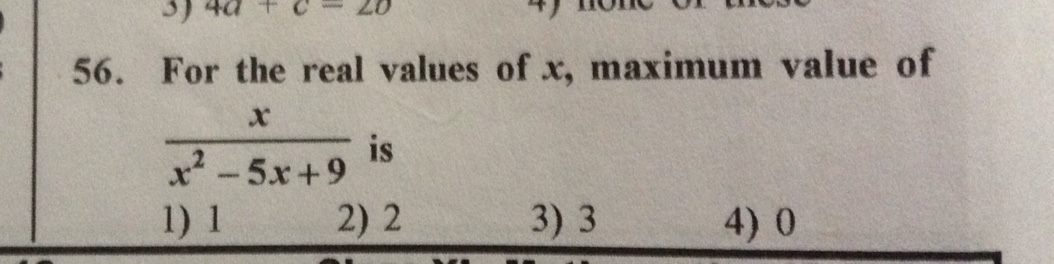
1 Answer
Oct 14, 2017
The answer is
Explanation:
I would call this
Taking the derivative, we get
#y' = (1(x^2 - 5x + 9) - x(2x -5))/(x^2 -5x + 9)^2#
#y' = (x^2 - 5x + 9 - 2x^2 + 5x)/(x^2 - 5x+ 9)^2#
#y' = (-x^2 + 9)/(x^2 - 5x + 9)#
Maximums and minimums will occur when the derivative equals
#0 = 9 - x^2#
#0 = (3 + x)(3 -x)#
#0 =-3 or 3#
If we select test points, we see that points in
#3/(3^2 - 15 + 9) =3/3 = 1#
Hopefully this helps!

