How do you write the rectangular equation #x^2+(y-2)^2=4# in polar form?
1 Answer
Oct 23, 2017
Expand the square.
Use
Solve the quadratic to obtain an equation of
Explanation:
Given:
Here is a graph of the original equation:
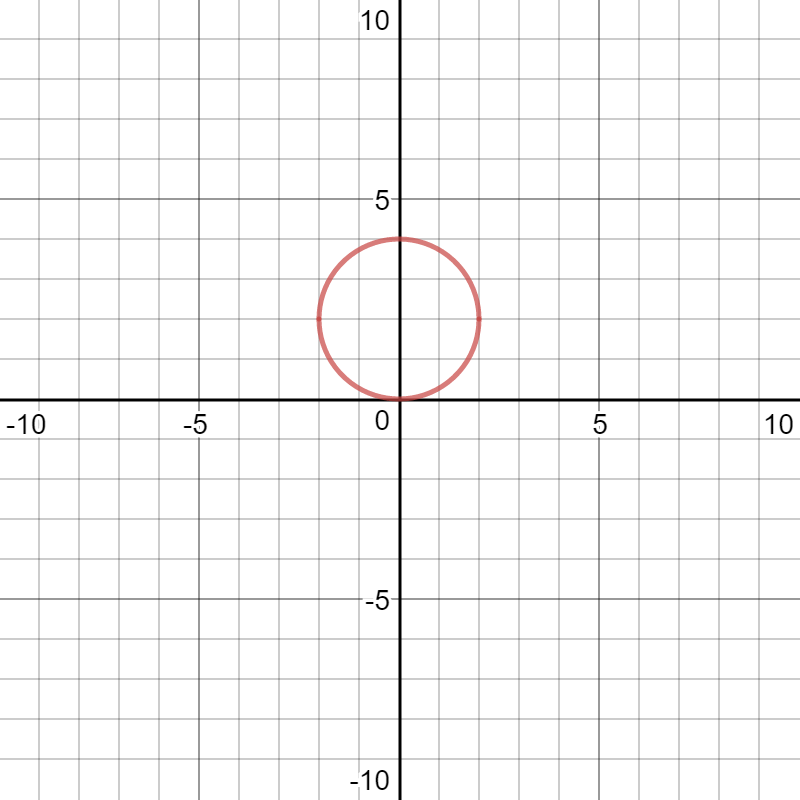
Expand the square:
Use
Combine like terms:
We can discard a common factor of r, because it is only the trivial root
Here is a graph of the converted equation:
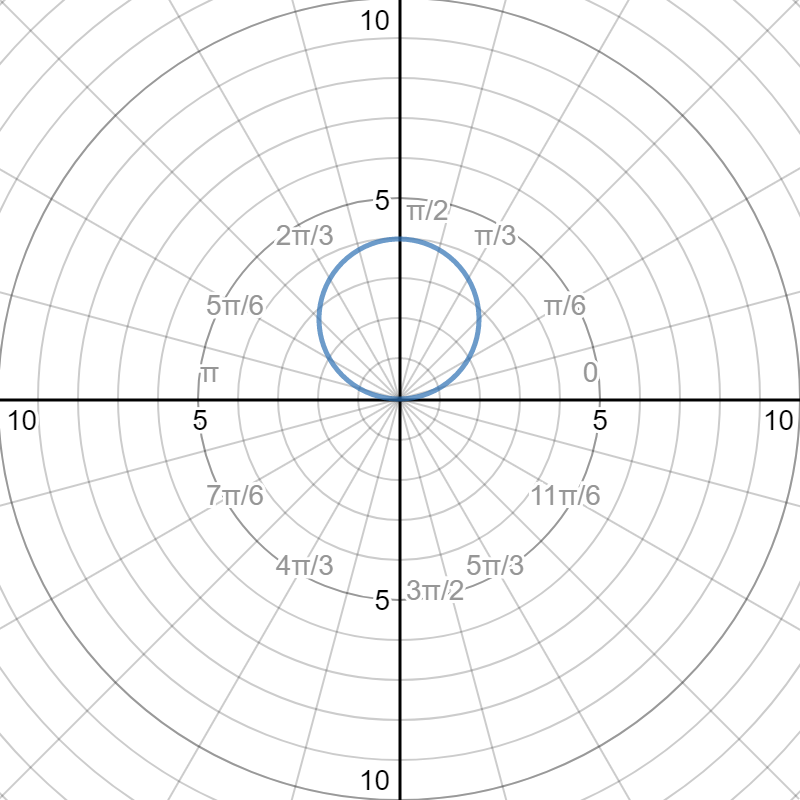
Please observe that the graphs are identical.
