How do you find the area of one petal of #r=cos5theta#?
2 Answers
Ans =
Explanation:
graph{y=cos(5x) [-2.075, 2.076, -1.008, 1.069]}
We first consider the graph y = cos(5x), and considering the roots, this is where each individual petal start and end in r = cos(5
Roots; cos(5
5
Hence to find the area of one petal, we can consider the petal that lies between
Now we can use
r = cos(5
letting z = cis(
z +
Hence
(or via considering
Hence our integral becomes;
Hence via evaluating this simple integral;
Area =
Explanation:
The polar curve is:
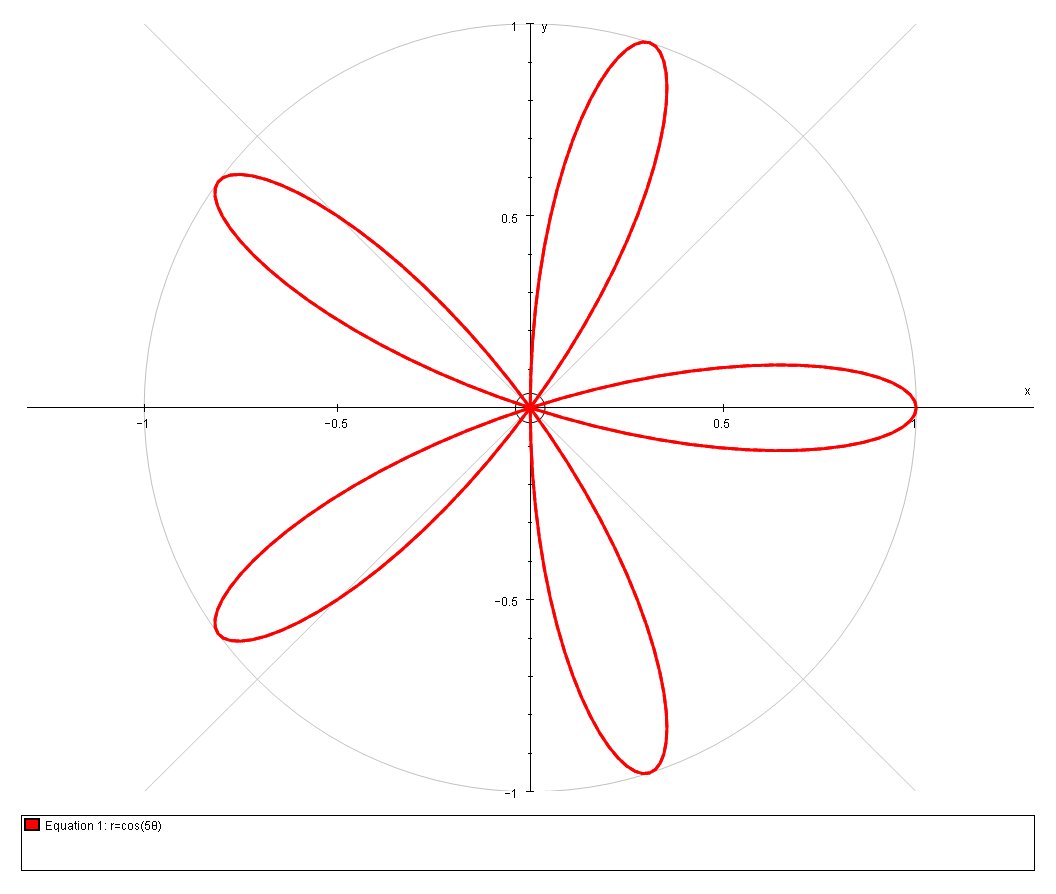
We calculate area in polar coordinates using :
# A = 1/2 \ int_alpha^beta \ r^2 \ d theta #
In order to calculate the area bounded by a single petal we would need to calculate the correct bounding angles, or we can calculate the entire area as we sweep through
Thus, the enclosed area is:
# A = 1/2 \ int_(0)^(pi) \ (cos5theta)^2 \ d theta #
Note that the entire area is swept out over the partial region
Now, Using the identity:
# cos 2A -= 2cos^2A -1 #
This becomes:
# A = 1/2 \ int_(0)^(pi) \ (1+cos10theta)/2 \ d theta #
# \ \ \ = 1/4 \ int_(0)^(pi) \ (1+cos10theta) \ d theta #
# \ \ \ = 1/4 \ [theta + (sin10theta)/10]_0^(pi) #
# \ \ \ = 1/4 \ { (pi+(sin10pi)/10) - (0+sin0) } #
# \ \ \ = 1/4 \ (pi+0 - 0) #
# \ \ \ = pi/4 #
This is the area of all five petals, so the area of a single petal is
# A_1 = A/5 = pi/20 #


