How can you do these types of problems quickly?
For A for example I know that one answer is pi/6 but how would I quickly know that the other solution is 5pi/6 without having to draw the unit circle?
Is there a shortcut to find the two solutions quickly when it asks for the solutions from 0 to 2pi? It seems very impractical to have to write down the entire unit circle just to solve these types of problems.
One other way is to use a calculator but my quiz doesn't allow me to use a calculator for these types of problems
For A for example I know that one answer is pi/6 but how would I quickly know that the other solution is 5pi/6 without having to draw the unit circle?
Is there a shortcut to find the two solutions quickly when it asks for the solutions from 0 to 2pi? It seems very impractical to have to write down the entire unit circle just to solve these types of problems.
One other way is to use a calculator but my quiz doesn't allow me to use a calculator for these types of problems
1 Answer
Please see below.
Explanation:
There are three things required for this.
- You should know the trigonometric ratios, at least of angles relating to first quadrant and if possible remember well the entire unit circle of trigonometric ratios (shown below).
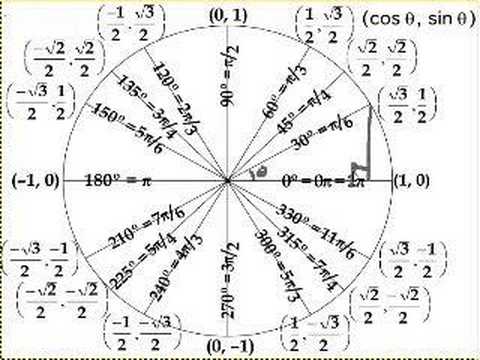 https://www.youtube.com/watch?v=6Qv_bPlQS8E
https://www.youtube.com/watch?v=6Qv_bPlQS8E - You should also know in which quadrants each of the trigonometric ratios are positive (in others, it will be negative). Well every ratio is positive in
Q1 , but sine and cosecant ratios are positive inQ2 too, tangent and cotangent are positive inQ3 too and cosine and secant are positive inQ4 too.
For
Q2 subtract angle from180^@ , forQ3 add angle to180^@ and forQ4 subtract angle from360^@ or0^@ .For example, for
sinx=1/2 , we knowx=30^@ , but as sine ratio is positive inQ2 too, other angle would be180^@-30^@=150^@ too. Similarly2tanx-5=1 meanstanx=3 and so iftanalpha=3 and alpha is inQ1 , the angle inQ3 would bealpha+180^@ . Similarly ascosx=sqrt2/2=cos45^@ and hencex=45^@ and360^@-45^@=315^@ , as cosine ratio is positive inQ4 .
The above should serve the purpose most of the time. However, last but not the least, if possible, remember the pattern (or graph) of the trigonometric ratios at least in the range
