What is the range of the function #h(x) = ln(x+6)#?

Question

5391 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-16T22:36:15

Answer: Using Monotony/continuity & Domain: #h(Dh)=R#

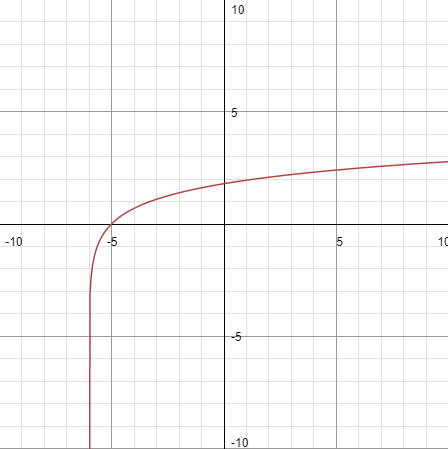
#h(x) = ln(x+6)# , #x>##-6#

#Dh=(-6,+oo)#

#h'(x)=1/(x+6)##(x+6)'##=1/(x+6)# #>0#, #x> -6#
So that means that #h# is strictly increasing ↑ in #(-6,+oo)#

#h# is obviously continuous in #(-6,+oo)# as composition of #h_1#(x)=x+6 & #h_2#(x) = #lnx#

#h(Dh)=h(#(-6,+oo)#)#= (#lim_(xrarr-6)h(x)#,#lim_(xrarr+oo)h(x))# #=(-oo,+oo)##=R#

because #⋅##lim_(xrarr-6)h(x)#= #lim_(xrarr-6)ln(x+6)#

#x+6=y#
#xrarr-6#
#yrarr0#

#= lim_(yrarr0)lny# #=-oo#

#⋅##lim_(xrarr+oo)h(x)#=#lim_(xrarr+oo)ln(x+6)##=+oo#

Note: you can also show this using the reverse #h^-1# function. (#y=ln(x+6)=>......)#