Solving this triangle?

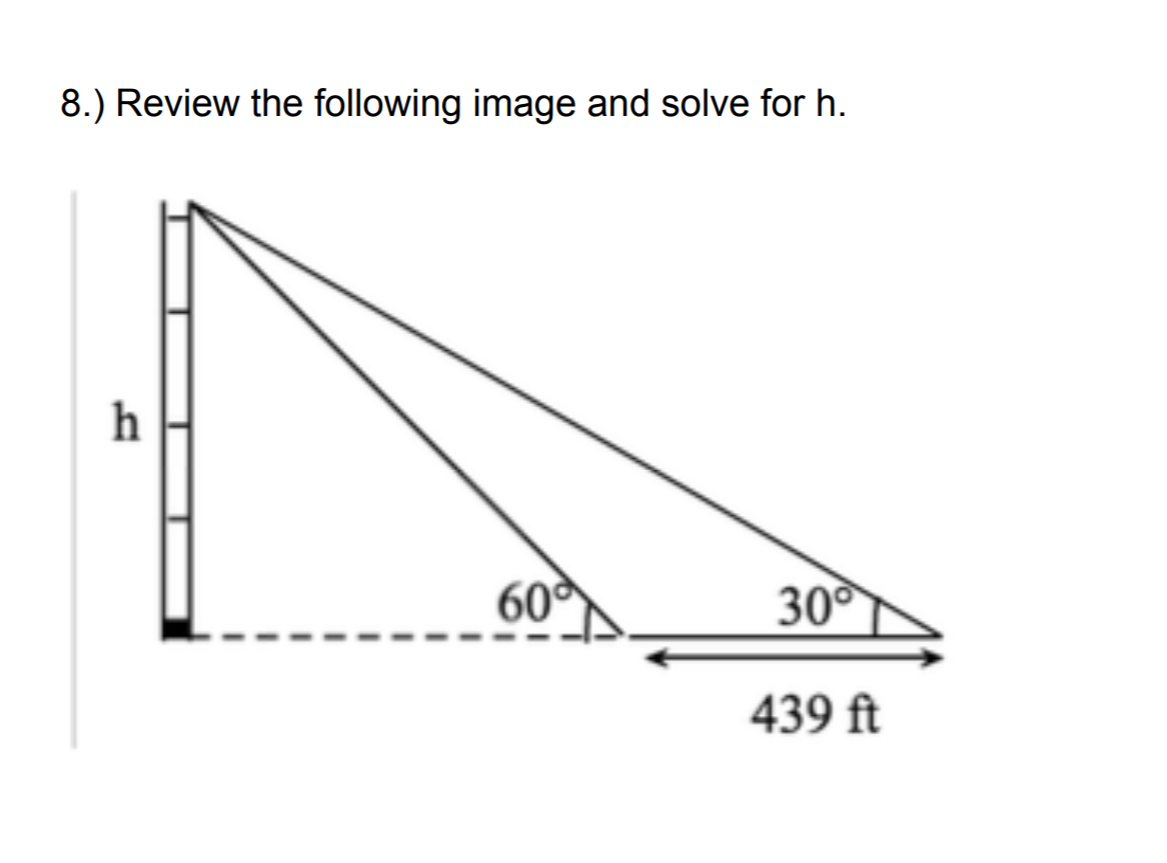
enter image source here

Solving for h ?

Thanks friends

1 Answer
Noah G
Dec 4, 2017

Approximately #380.2# feet.

Explanation:

We can write a system of equations. If we let #x# be the distance on the base from the right angle to the #60^@# angle, then we can say:

#h/(x + 439) = tan(30^@)#

And

#h/x = tan(60^@)#

Thus:

#h = tan(30^@)(x + 439)#

Substituting:

#tan(30^@)(x + 439) = xtan(60^@)#

#1/sqrt(3)x + 1/sqrt(3)(439) = xsqrt(3)#

#1/sqrt(3)x - xsqrt(3) = -1/sqrt(3)439#

#x(1/sqrt(3) - sqrt(3)) = -1/sqrt(3)439#

#x = (-1/sqrt(3) 439)/(1/sqrt(3) - sqrt(3))#

#x = (-1/sqrt(3)439)/(-2/sqrt(3))#

#x = 439/2#

Thus, the entire length of the side measures #439/2 + 439 = 1317/2#.

Therefore,

#h/(1317/2) = tan(30^@)#

#h = 1317/2(1/sqrt(3))#

#h = 1317/(2sqrt(3))#

This can be calculated using a calculator.

#h ~~ 380.2" ft"#

Hopefully this helps!

Related questions
Impact of this question
933 views around the world
You can reuse this answer
Creative Commons License