Question #222eb
1 Answer
Dec 10, 2017
Explanation:
The general expression of the Taylor series of
For
Then:
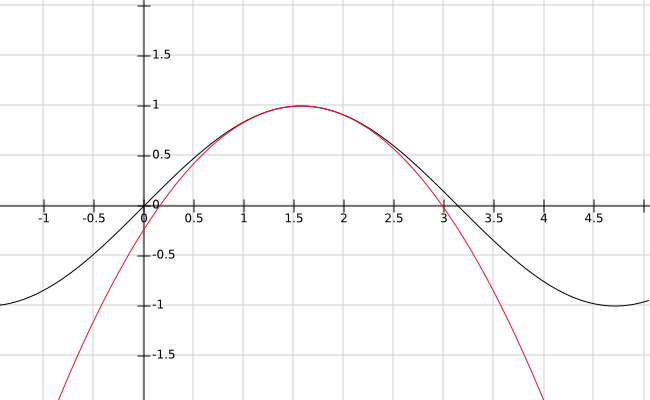
We can also note that:
so we can use the MacLaurin expansion of
The general expression of the Taylor series of
For
Then:

We can also note that:
so we can use the MacLaurin expansion of