Question

What is the inverse of f(x)=4x+3 ?

Answer 1

`f^-1 (x) = 1/4 x - 3/4`

Explanation:

When finding the inverse:
Swap the `x` with `f^-1 (x)` and swap `f(x)` with `x`:

`=> x = 4f^-1 (x) + 3`

`=> x -3 = 4f^-1 (x)`

`=> (x-3)/4 = f^-1 (x)`

`=> 1/4 x -3/4 = f^-1(x)`

Answer 2

`f^(-1) x= 1/4 x -3/4`

Explanation:

Let y=f(x)=4x+3. Now interchange x and y and then solve for y. Accordingly, x =4y+3
Therefore 4y= x-3
which gives y=`f^(-1) x=1/4` (x-3)= `1/4 x -3/4`

Answer 3

It's the first answer.

Explanation:

To find the inverse of a function, invert x and y.
Then, isolate y and you have it.

So, our initial function is `f(x)=4x+3`.
We can rewrite it as `y=4x+3`,

Then, invert x and y:
`x=4y+3`

And now, isolate y:
`x-3=4y`
`y=1/4(x-3)`
`y=1/4x-3/4`

And finally, replace y with the inverse function notation:
`f^-1=1/4x-3/4`

So, it's the first answer.

Answer 4

`f^-1(x)=1/4x-3/4`

Explanation:

Consider this as a function machine, where we put `x` into the machine, and get `f(x)` out.

If we have this, what do we need to do to `f(x)` to get `x` back out?

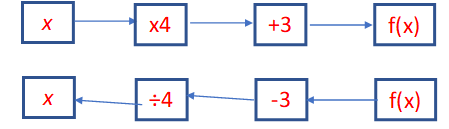
so if `f(x)=4x+3` then
`f^-1(x)=(x-3)/4`
`f^-1(x)=1/4x-3/4`