Question

Question #3a139

Answer 1

Remember what the equal sign really means, including what it means we can do, perhaps using an analogy and an example equation.

Explanation:

For example, let's say we have `2x + 7 = 5`.

Here, have a look at what's being presented.

The equal sign tells us that they're equal. They are the same.

Whatever `2x + 7` is, it is the same as `5`.

Maybe we do not know what `x` is at the moment, but we do know this equation. Think of it as a balance (forgive my bad drawings):

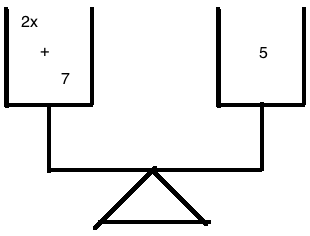
So, what can we do to find out what `x` is?

Here's an idea: how about if we add `-7` to both sides?

I mean, `-7` = `-7`; the number we'll be giving on one side is the same as the number we'll be giving on the other side, right?

Right. Looking back at the equations, we now have:

`2x + 7 + (-7) = 5 + (-7)`

Just like we asked for: adding `-7` to both sides.

Now that we have `-7` in there, shouldn't we... do something? Yeah, let's simplify the equation!

`2x = -2`

Whoa, whoa. Take a look at what happened. On the left side, `7` and `(-7)` cancel each other out. On the right side, we evaluated `5 - 7 = -2`. Our balance now looks like this:

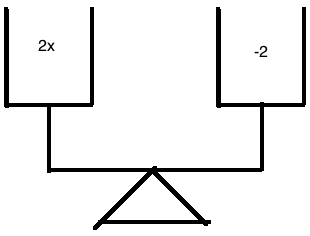
Huh, that might be unsettling to look at. What exactly does `2x` mean? Well, whenever there's a multiplication between two things, we can usually imagine it as some sort of area:

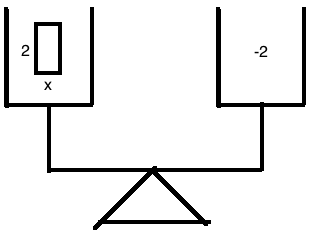
And the other number, too, and the best part is we can choose what the lengths and widths should be. Let's try `-1` and `2`:

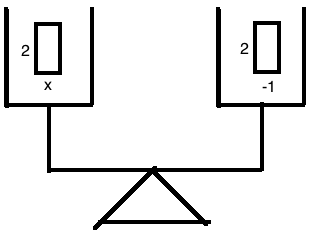
Then... well, we just want `x`, and not twice of `x`... why not cut it into half? Split it?

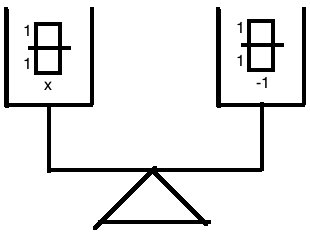
So... looking at this algebraically, we know have that twice of `x` is the same as twice of `-1`:

`2x = 2 * -1`:

If twice of a thing is the same of twice of another thing... wouldn't it be reasonable to say that those two things are exactly the same thing?

`x = -1`

We had thrown away half of each in the balance:

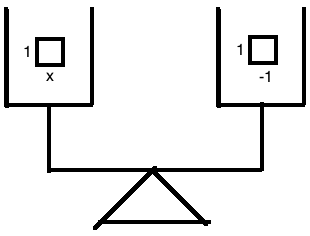
Well, the balance itself tells us `x * 1 = -1 * 1`, but any number times `1` is just the number itself, right?

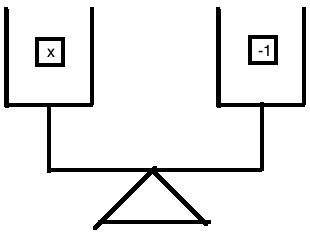
So, we're done! `x = -1`. You could redo this with any other two-step equation.