Question

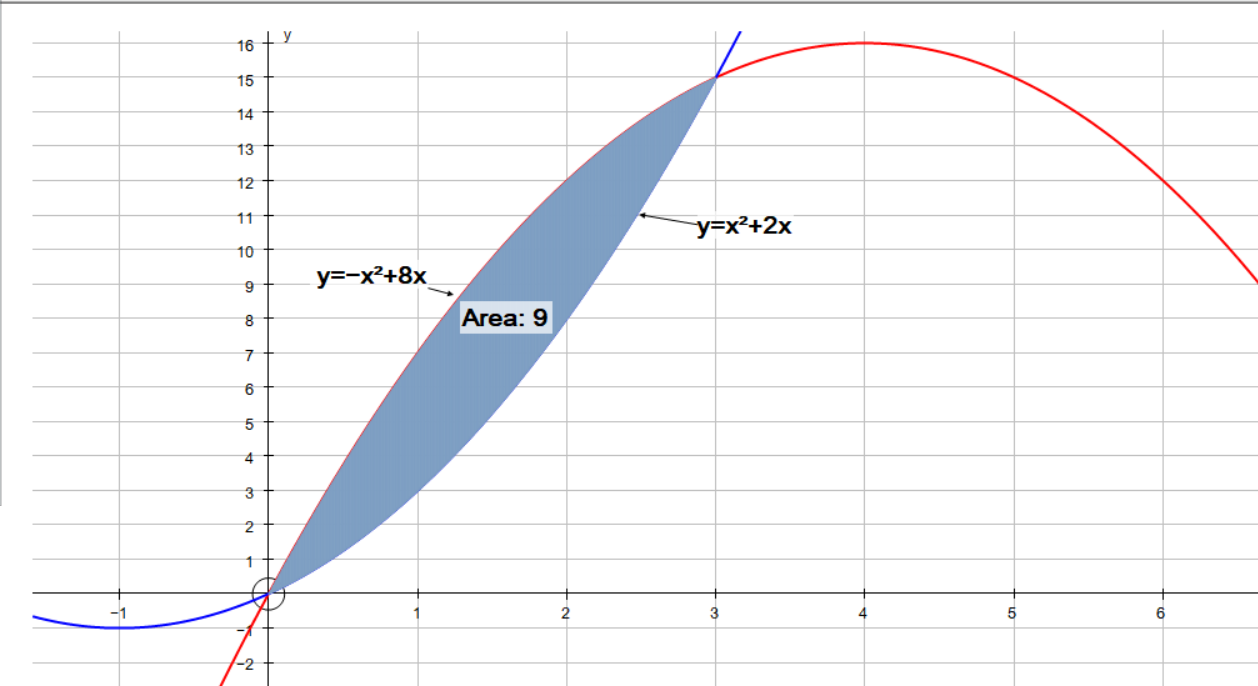
What is the area of the region bounded between the graphs of y= -x^2 + 8x and y =x^2 + 2x?

Answer 1

The area is `9` square units

Explanation:

First step is always to find intersection points. These will be the endpoints of the area we must find.

Since both functions have `y` isolated, we can solve the system of equations

`{(y = -x^2 + 8x), (y = x^2 + 2x):}`

readily.

`x^2 +2x= -x^2 + 8x`

`2x^2 - 6x = 0`

`2x(x - 3) = 0`

`x = 0 or 3`

If we test a random point in this interval into both of the functions, we find that `y= -x^2 +8x` has a higher value than `y =x^2 + 2x`. Therefore the expression for area will be

`A = A_"highest curve" - A_"lowest curve"`

`A = int_0^3-x^2 +8x- (x^2 + 2x)dx`

`A = int_0^3 -x^2 + 8x - x^2 - 2x dx`

`A = int_0^3 -2x^2 + 6x dx`

The integral is given by

`A = [-2/3x^3 + 3x^2]_0^3`

`A = -2/3(3)^3 + 3(3)^2 - 0`

`A = -2/3(27) + 3(9)`

`A = -18 + 27`

`A = 9`

Hopefully this helps!

Answer 2

`9` square units.

Explanation:

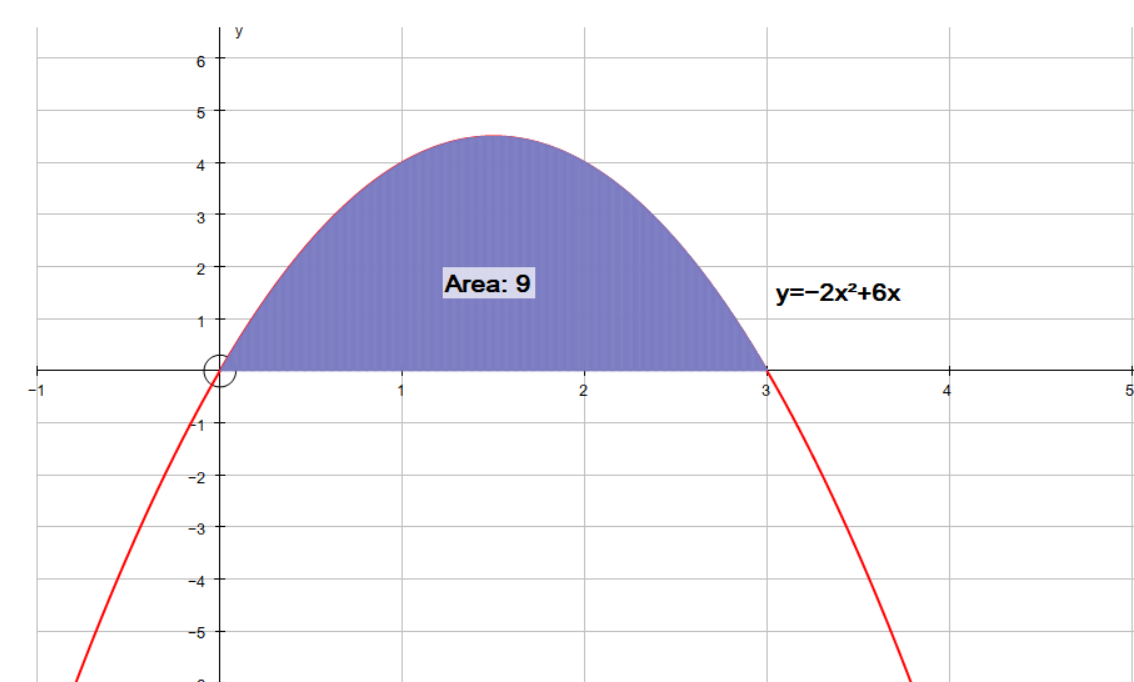
If you observe the graph of these two functions together, the area sought is between the two points of intersection. Therefore if we equate the functions together, we can then just find the area between the single function and the x axis.

`-x^2+8x=x^2+2x`

`-2x^2+6x`

The points of intersection are:

`-2x^2+6x=0`

`2x(x-3)=0=>x=3 and x=0`

So our integral is:

`A=int_(0)^(3)(-2x^2+6x)dx=[-2/3x^3+3x^2]_(0)^(3)`

Plugging in the upper and lower bounds:

`A=[-2/3(3)^3+3(3)^2]-[-1/3(0)^3+3(0)^2]`

`A=[-54/3+27]=[9]`

Area `9` square units

Graph of the two separate function with area 9 sq units.

Graph of single function with area 9 sq units.