Question

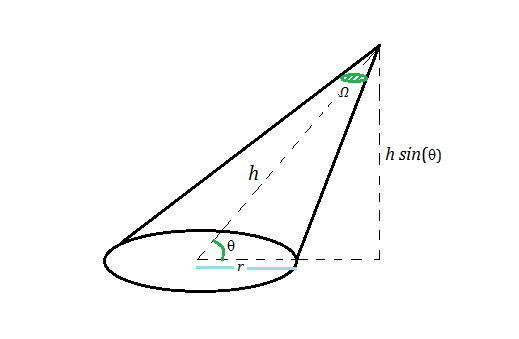
What is formula for solid angle labeled in the given figure as `Omega`?

Answer 1

The solid angle `Omega=pisintheta(r/h)^2` steradians.

Explanation:

In simple language, one can say that a solid angle is a measure of how big an object looks to an observer. Just consider sun. Although sun is very large as compared to moon, to an observer on Earth it appears almost of the same size as that of moon.

Imagine we are standing at the center of a large sphere. Its surface area is `4pir^2`. Just like radian, where for angle we divide arc size by `r` to get angle in radians, we can say that the entire surface area of the sphere subtends a solid angle of `(4pir^2)/r^2=4pi` steradians at the center. We can say that the angle subtended by a surface area `A` at a distance of `r` is `A/r^2` steradians.

Hence, a solid angle `Omega` is the angle subtended by a surface, say given by the circle (in the image shown in the question) with radius `r` at a point situated at a distance of `h` at an angle `theta` as shown in the image.

However, observe that as we are looking at the circle at an angle and hence it will appear as an ellipse. The appearance is as shown in the image below. Note that while major axis will be same as `2r`, the minor axis will be `2rcos(90^@-theta)=2rsintheta`.

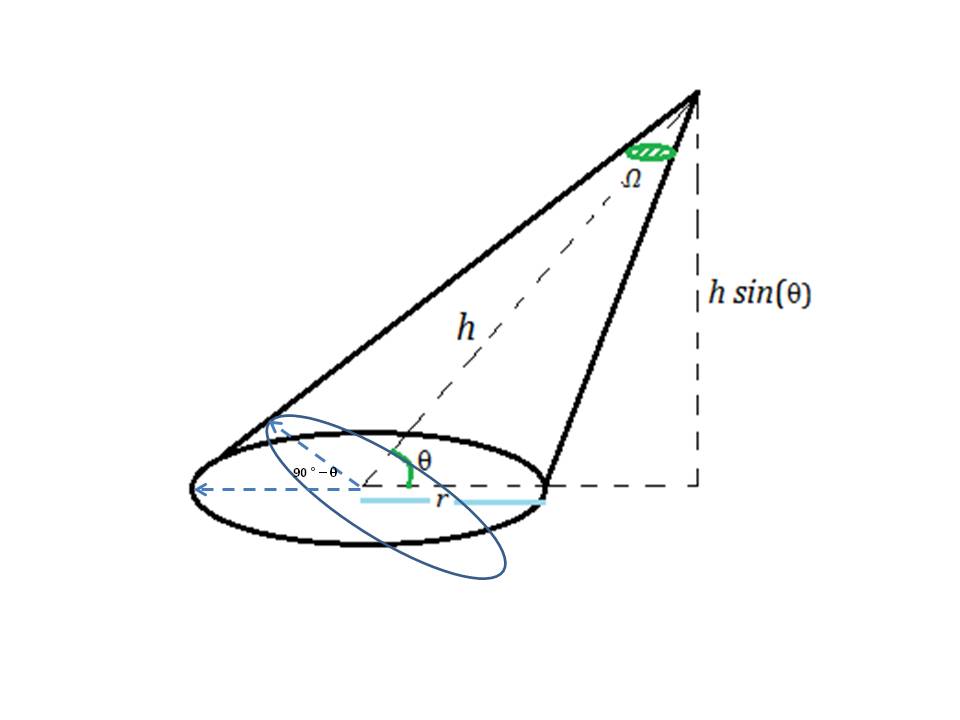
As area of ellipse is given by `piab`, the area would be

`pir^2sintheta`.

Hence, the solid angle `Omega=(pir^2sintheta)/h^2=pisintheta(r/h)^2` steradians.