Question

Estimate the area under `y=x^2+x` from `x=0.2` to `x=1` using Simpson's rule with `6` strips?

Answer 1

`A = int_0.2^1 \ x^2+x \ dx ~~ 0.810667`

Explanation:

We have:

`y = x^2+x`

We want to estimate `int \ y \ dx` over the interval `[0.2,1]` with `6` strips; thus:

`Deltax = (1-0.2)/6 = 2/15`

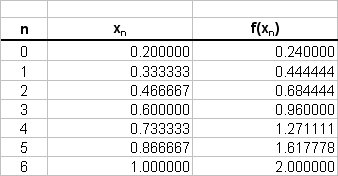
The values of the function are tabulated as follows;

Simpson's Rule

Using Simpson's Rule we can estimate the area using best fit quadratics, which generally gives an accurate estimation. We use the formula:

`int_a^b \ f(x) \ dx ~~ h/3{(y_0+y_n)+4(y_1+y_3+...+y_(n-1))+2(y_2+Y_4+...+y_(n-2))}`

So we have:

`A = int_0.2^1 \ x^2+x \ dx`
`\ \ \ ~~ 0.133333/3 { 0.24 + 2 + 4(0.444444 + 0.96 + 1.617778)+2(0.684444 + 1.271111)}`
`\ \ \ = 0.044444 { 2.24 + 4(3.022222)+ 2(1.955556)}`
`\ \ \ = 0.044444 { 2.24 + 12.088889+3.911111 }`
`\ \ \ = 0.066667 * 18.24`
`\ \ \ = 0.810667`

Actual Value

For comparison of accuracy:

`A = int_0.2^1 \ x^2+x \ dx`
`\ \ \ = [x^3/3+x^2/2]_0.2^1`
`\ \ \ = (1/3+1/2) -(1/375+1/50)`
`\ \ \ = 304/375`
`\ \ \ = 0.810666666...`

Notes

We note that to the accuracy of calculation Simpsons rules produced an exact answer. This is no conicenice. The function we are integrating is quadratic, and Simpsons rils works by estimating the area under the best fit quadratic of the adjacent points and therefore it provided, in this case, the exact answer.