If #sqrt(sinx) + cosx = 0#, the what is the value of #sinx#?
3 Answers
Explanation:
Squaring,
Completing Square on the L.H.S., we find,
But because of
See below.....
Explanation:
#sqrt(sinx)+cosx=0#
#=>sqrtsinx=-cosx#
#=>sinx=cos^2x#
#=>sinx=1-sin^2x#
#=>sin^2x+sinx-1=0#
#=>m^2+m-1=0" "" where"" " m=sinx#
Now,
Solution of

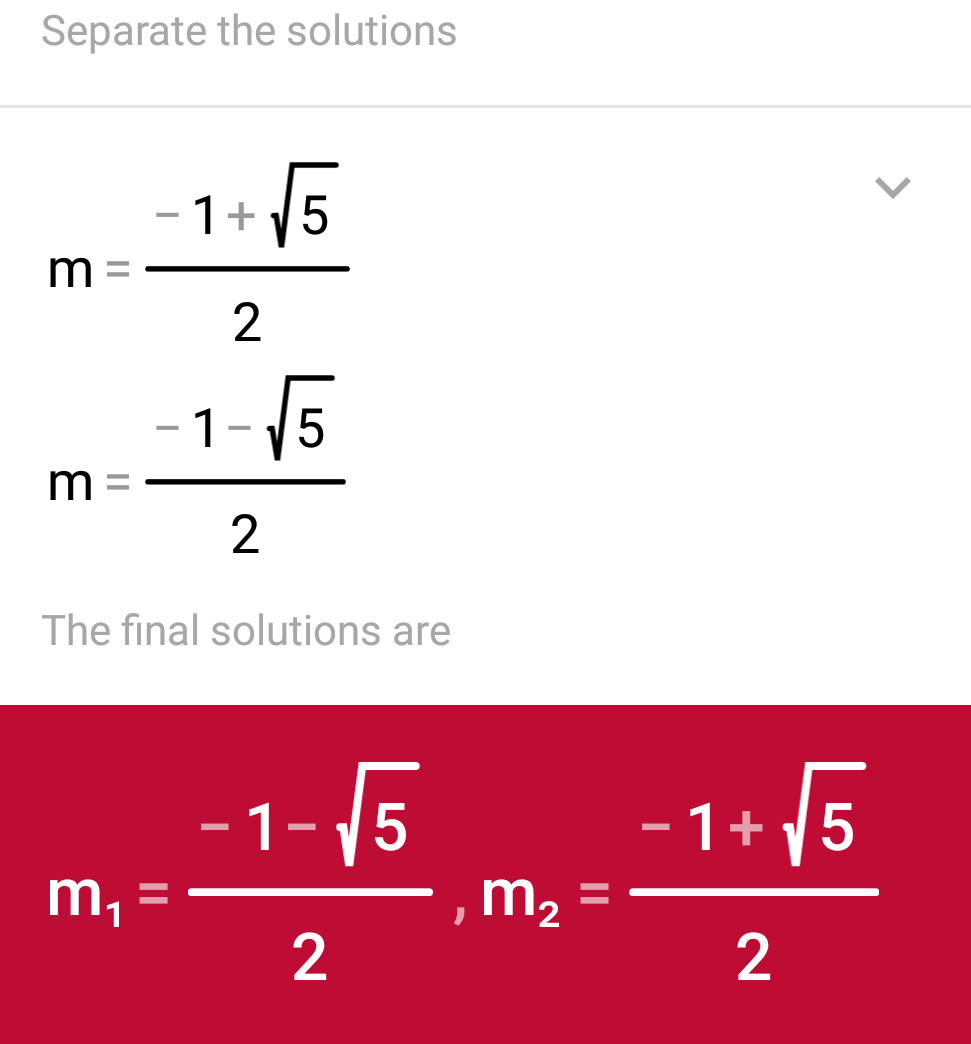
This is the answer for
#sinx=(sqrt5-1)/2# as#-1 < sinx < +1#
Graphical representation:-
graph{x^2+x-1 [-7.83, 12.17, -4.81, 5.19]}
We have to manipulate the equation to a more manageable form, and then solve it.
Explanation:
If
So we have
Now this is a quadratic equation in
We get two solutions:
But now, we should observe that
Note 1: We have to be careful not to introduce false solutions. Say we have
Note 2: The solution


