Question

If `sqrt(sinx) + cosx = 0`, the what is the value of `sinx`?

Answer 1

`sinx=-1/2+sqrt5/2=(sqrt5-1)/2`.

Explanation:

`sqrtsinx+cosx=0`,

`rArr sqrtsinx=-cosx`,

Squaring, `sinx=cos^2x=1-sin^2x, or,`

`sin^2x+sinx=1`.

Completing Square on the L.H.S., we find,

`sin^2x+sinx+1/4=1+1/4, i.e.,`

`(sinx+1/2)^2=(sqrt5/2)^2`,

`:. sinx+1/2=+-sqrt5/2`, which gives,

`sinx=-1/2+-sqrt5/2`.

But because of `sqrtsinx, sinx lt 0` is not admissible.

`:. sinx=-1/2+sqrt5/2=(sqrt5-1)/2`.

Answer 2

See below.....

Explanation:

`sqrt(sinx)+cosx=0`
`=>sqrtsinx=-cosx`
`=>sinx=cos^2x`
`=>sinx=1-sin^2x`
`=>sin^2x+sinx-1=0`
`=>m^2+m-1=0" "" where"" " m=sinx`

Now,
Solution of `color(red)m` is

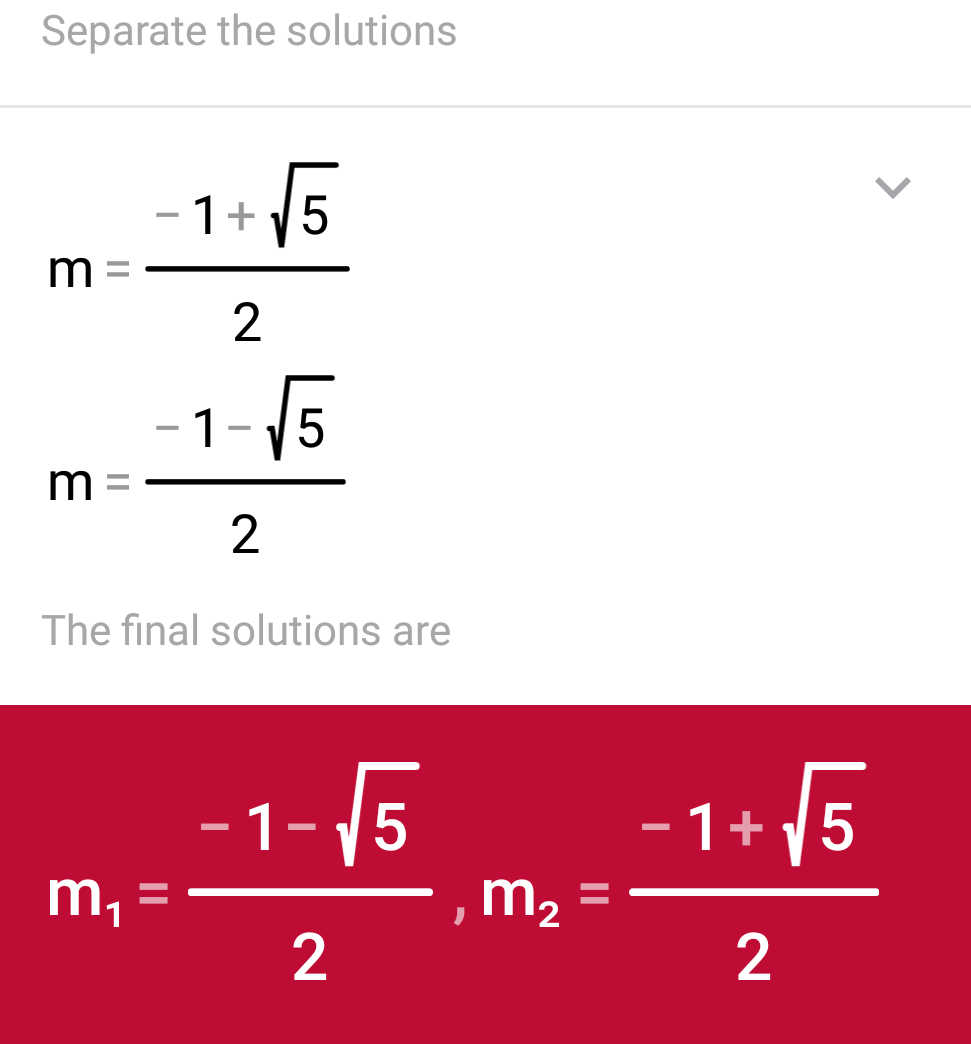
This is the answer for `sinx=(sqrt5-1)/2` as `-1 < sinx < +1`
Graphical representation:-

graph{x^2+x-1 [-7.83, 12.17, -4.81, 5.19]}

Answer 3

We have to manipulate the equation to a more manageable form, and then solve it.

Explanation:

If `sqrt(sin x) = -cos x` we can raise this to the square (be careful here, read Note 1 below!)

So we have `sin x = (-cos x)^2= cos^2 x`, but `sin^2x + cos^2x=1`, so we can use `cos^2x = 1- sin^2x` and we can replace `cos^2x`:

`sin x= 1-sin^2x` or the same `sin^2x + sin x -1 = 0`

Now this is a quadratic equation in `sinx`, we may call `sinx=y` and then solve:

`y^2+y-1=0`

We get two solutions:

`y_1=(-1+sqrt(5))/2` and `y_2=(-1-sqrt(5))/2`

But now, we should observe that `y_2 <-1` and it can't be the a value for `sinx` (see Note 2 below). The other value `y_1=(-1+sqrt(5))/2` however is a `positive` number within the range of `sinx`, so that's a solution for the equation.

Note 1: We have to be careful not to introduce false solutions. Say we have `y=-1`, we then know that `y^2=1`, but when solving this last one we obtain two solutions `y=-1` (the original one) and `y=1` (a false one). This is because `y=-1 => y^2 = 1` but not the other way around

Note 2: The solution `y` of the equation above must be a value within the range `-1` and `1`, and be `y >=0` to be possible to take the square root. But `2 < sqrt(5) < 3` and so `1 < -1+sqrt(5) <2` and then `0 < y_1= (-1+sqrt(5))/2 < 1`