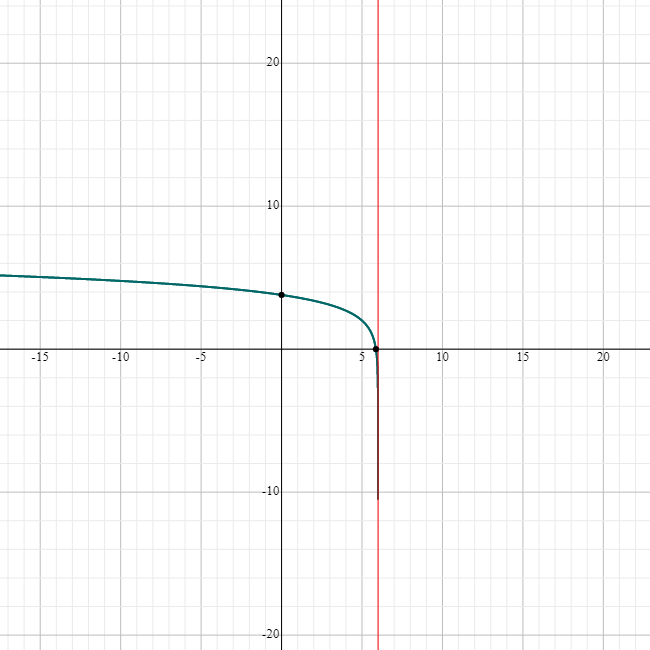
#f(x)=ln(6-x)+2#
- For #f# to be defined in #RR# we need:
#6-x>0# #<=># #x<6#
Justifications: [ because domain of #y=lnx# is #(0,+oo)# and you have composition of functions #g(x)=lnx# , #h(x)=6-x# so you need #x##in##D_h=RR# and #h(x)##in##D_g=(0,+oo)# ]
As a result the domain of #f# is #D_f=(-oo,6)#
For the range i will work with monotony and continuity of the function.
#f# is continuous/differentiable in #D_f# as a function of the compositions mentioned above.
#f'(x)=(ln(6-x)+2)'=1/(6-x)(6-x)'# #=-1/(6-x)=1/(x-6)<0#, if #x<6#
(you can see that by plugging any value #<6# in #f'#)
Therefore #f# is strictly decreasing in #(-oo,6)#
[ Alternative for finding monotony (incase you are not familiar with derivatives):
- Supposed we have #x_1# , #x_2# #in##(-oo,6)# with #x_1##<##x_2#
Then we will have #-x_1>##-x_2#
#<=># #6-x_1##>6-x_2#
#lnx# is increasing in #(0,+oo)# so we can plug #ln# in each side
#<=># #ln(6-x_1)##>ln(6-x_2)#
#<=># #ln(6-x_1)+2##>ln(6-x_2)+2#
#<=># #f(x_1)>f(x_2)# #-># #f# strictly decreasing in #(-oo,6)# ]
So we have the following table:
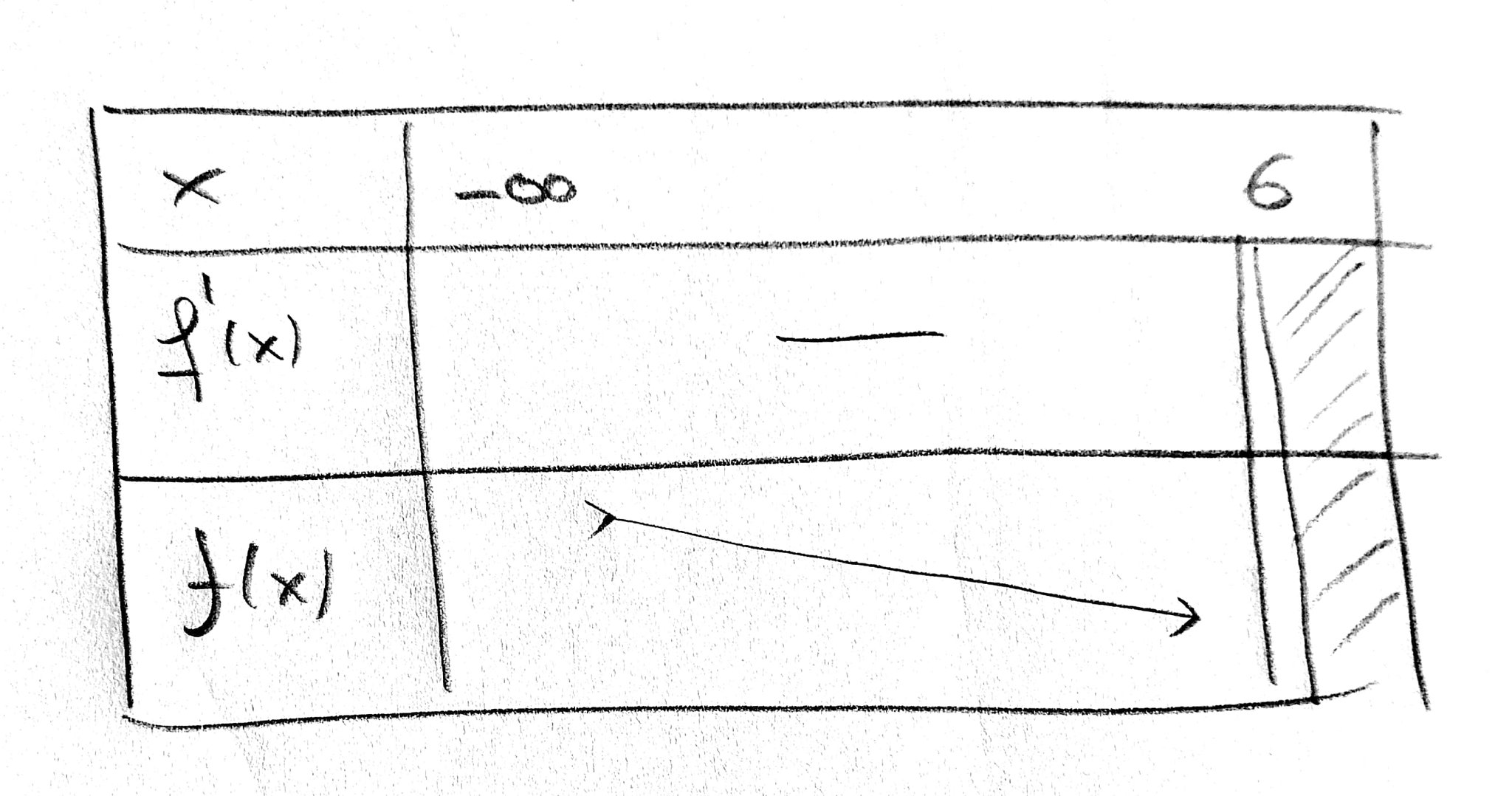
Range will be the ''image'' of the domain,
#f(D_f)=##f(##(-oo,6))# #=# #(lim_(xrarr6^(-))f(x),lim_(xrarr-oo)f(x))# #=#
#(-oo,+oo)=RR#
because
- #lim_(xrarr6^(-))f(x)=lim_(xrarr6^(-))##(ln(6-x)+2)#
Set #6-x=u#
#x->6^-#
#u->0#
#=# #lim_(urarr0)(lnu+2)=-oo+2=-oo#
- #lim_(xrarr-oo)f(x)=lim_(xrarr-oo)(ln(6-x)+2)#
Set #6-x=y#
#x->-oo#
#y->+oo#
#=# #lim_(yrarr+oo)(lny+2)=+oo+2=+oo#
Here is the graph of the function:
#f(x)=ln(6-x)+2# , #x<6#