How do you solve x^2-12x+5=0 by completing the square?
3 Answers
just add and subtract
Explanation:
so we have
therefore
so
hope u find it helpful :)
Explanation:
"using the method of "color(blue)"completing the square"
• " the coefficient of the "x^2" term must be 1 which it is"
• " add/subtract "(1/2"coefficient of x-term")^2" to"
x^2-12x
rArrx^2+2(-6)xcolor(red)(+36)color(red)(-36)+5=0
rArr(x-6)^2-31=0
rArr(x-6)^2=31
color(blue)"take the square root of both sides"
rArrx-6=+-sqrt31larrcolor(blue)"note plus or minus"
rArrx=6+-sqrt31
See explanation
Explanation:
For a shortcut method see https://socratic.org/s/aMzZC8RW
This is actually changing
Where
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This uses the 'perfect square' but modifies it so that it matches the given equation. A bit like the logic of
Perfect square
Compare:
Using Point(1) and Point(2) now we have:
We now have to change the standard form so that it has the same overall value of the given equation. We need to change
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
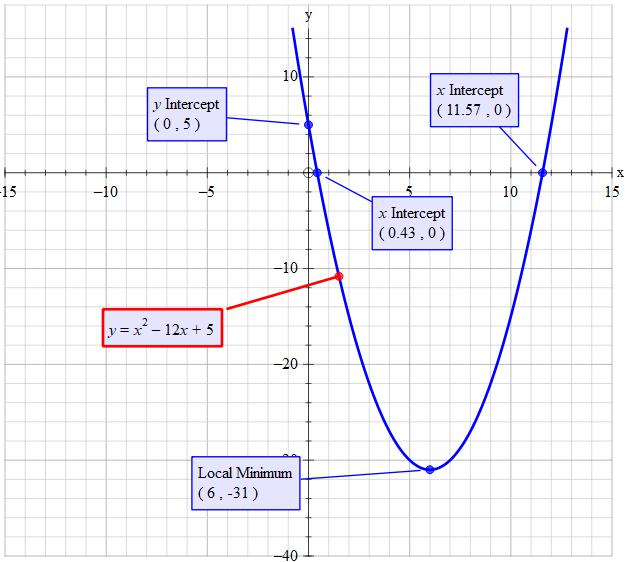
Vertex
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For x-intercepts
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
From
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 Tony B
Tony B

