Question

Question #f307f

Answer 1

`n=3,l=2,m_l = 1, m_s = -1/2`

Explanation:

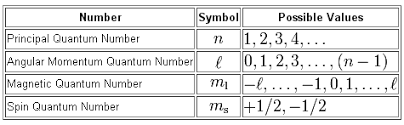
The first quantum number set given to you is not correct because the spin quantum number, `m_s`, can only take two possible values.

`m_s = {+1/2, - 1/2}`

So the quantum number set that has

`m_s = +1`

cannot be used to describe the location and the spin of an electron inside an atom.

The second quantum number set is also incorrect because the angular momentum quantum number, `l`, cannot take the same value as the principal quantum number, `n`.

Similarly, the third quantum number set is incorrect because the angular momentum quantum number cannot take a negative value.

More specifically, the angular momentum quantum number can take

`l = {0, 1, ..., n-1}`

So the quantum number set that has

`n=1, l =1`

is not valid because the value of the angular momentum quantum number is not possible given the value of the principal quantum number.

The set that has

`l = -3`

is not valid because of the negative value assigned to the angular momentum quantum number.

The fourth quantum number set is correct because all the four quantum numbers take accepted values.

`n = 3, l = 2, m_l = 1, m_s = -1/2`

This set describes an electron located in the third energy shell, in the `3d` subshell, let's say in the `3d_(xy)` orbital, that has spin-down.

The value of the magnetic quantum number, `m_l`, is valid here because this quantum number can take the possible values

`m_l = {-l, -(l-1),..., -1, 0, 1, ..., (l-1), l}`

So for

`l = 2`

you can have

`m_l= 1`

as a valid value for the magnetic quantum number.